Chapter 4 Examples
Wednesday, January 27, 1993
Theorem 4.1 Given a Cayley graph \(\Gamma = \Gamma(G, \Delta)\). View the standard module \(V \equiv \mathbb{C}G\) (the group algebra), so \[\left\langle \sum_{g\in G}\alpha_g g, \;\sum_{g\in G}\beta_g g\right\rangle = \sum_{g\in G}\alpha_g\overline{\beta_g}, \quad \textrm{with}\; \alpha_g, \beta_g\in \mathbb{C}.\] For any \(\theta\in X(G)\), write \[\hat{\theta} = \sum_{g\in G}\theta(g^{-1})g.\] Then the following hold.
\[\Delta_\theta = \sum_{g\in \Delta}\theta(g).\] In particular, the eigenvalues of \(\Gamma\) are precisely \[\{\Delta_\theta \mid \theta\in X(G)\}.\]
Proof.
\[s:= \sum_{g\in G}\theta(g^{-1}) = \begin{cases} |G| & \text{if }\;\theta = 1\\ 0 & \text{if } \;\theta \neq 1. \end{cases}\] Pf. Clear if \(\theta =1\).
Let \(\theta \neq 1\). Then \(\theta(h)\neq 1\) for some \(h\in G\). \[s\cdot \theta(h) = \left(\sum_{g\in G}\theta(g^{-1})\right)\theta(h) = \sum_{g\in G}\theta(g^{-1}h) = \sum_{g'\in G}\theta(g'^{-1}) = s.\] Since \(\theta(h)\neq 1\), \(s = 0\).
Claim. \(\theta(g^{-1}) = \overline{\theta(g)}\) for every \(\theta\in X(G)\) and every \(g\in G\).
Since \(\theta(g)\in \mathbb{C}\) is a root of \(1\), \[|\theta(g)|^2 = \theta(g)\overline{\theta(g)} = 1.\] On the other hand, since \(\theta\) is a homomorphism, \[\theta(g)\theta(g^{-1}) = \theta(1) = 1.\] Hence \(\theta(g^{1}) = \overline{\theta(g)}\).
Now \[\begin{align} \langle \widehat{\theta_1}, \widehat{\theta_2}\rangle & = \sum_{g\in G}\theta_1(g^{-1})\overline{\theta_2(g^{-1})}\\ & = \sum_{g\in G}\theta_1(g^{-1})\theta_2(g)\\ & = \sum_{g\in G}\theta_1\theta_2^{-1}(g^{-1})\\ & = \begin{cases} |G| & \text{if}\quad \theta_1\theta_2^{-1} = 1\\ 0 & \text{if} \quad \theta_1\theta_2^{-1}\neq 1. \end{cases} \end{align}\] Since \(|G| = |X(G)|\) by Lemma 3.1, and \(\widehat{\theta_i}\)’s are orthogonal nonzero elements in \(V\), that form a basis of \(V\).
\[\begin{align} A\hat{\theta} & = A\left(\sum_{g\in G}\theta(g^{-1}g)\right)\\ & = \sum_{g\in G}\theta(g^{-1})(gg_1 + \cdots + gg_r) \quad (\Gamma(g) = \{gg_1, \ldots, gg_r\})\\ & = \sum_{i = 1}^r \left(\sum_{g\in G}\theta(g^{-1})(gg_i)\right)\\ & = \sum_{i=1}^r\left(\sum_{g\in G}\theta(g_ig_i^{-1}g^{-1})(gg_i)\right)\\ & = \sum_{i = 1}^r\left(\sum_{g\in G}\theta(g_i)\theta((gg_i)^{-1})gg_i\right)\\ & = \sum_{i = 1}^r\theta(g_i)\sum_{h\in G}\theta(h^{-1})h \\ & = \Delta_\theta\cdot \hat{\theta}. \end{align}\] Since \(\{\hat{\theta}\mid \theta\in X(G)\}\) forms a basis, the eigenvalues of \(\Gamma\) are precisely, \[\{\Delta_\theta\mid \theta\in X(G)\}.\]
This completes the proof.
Example 4.1 Let \(G = \langle a\mid a^6 = 1\rangle\), and \(\Delta = \{a, a^{-1}\}\). Pick a primitive 6-th root of 1, \(\omega\). Then
\[X(G) = \{\theta^i\mid 0\leq i\leq 5\} \quad \text{such that }\quad \theta(a) = \omega, \; \omega + \omega^{-1} = 1.\]
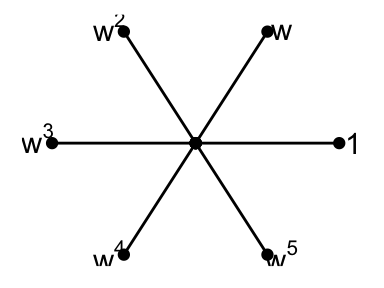\[\begin{array}{c | c | c}
\varphi\in X(G) & \varphi(a) & \Delta_\varphi = \theta(a) + \theta(a)^{-1}\\
\hline
1 & 1 & 2\\
\theta & \omega & \omega+\omega^{-1} = 1\\
\theta^2 & \omega^2 & -1\\
\theta^3 & \omega^3 = -1 & -2\\
\theta^4 & \omega^4 & -1\\
\theta^5 & \omega^5 & 1
\end{array}\]
\[\text{Spec}(\Gamma) = \begin{pmatrix} 2 & 1 & -1 & -2\\ 1 & 2 & 2 & 1\end{pmatrix}.\]
Example 4.2 \(D\)-cube, \(H(D,2)\). Let \[X = \{(a_1, \ldots, a_D)\mid a_i\in \{1,-1\}, \; 1\leq i\leq D\},\] \[E = \{xy\mid x, y\in X, \; x, y \text{: different in exactly one coordinate}\}.\] Also \(H(D,2)\) is a Cayley graph \(\Gamma(G, \Delta)\), where \[G = G_1\oplus G_2 \oplus \cdots \oplus G_D, \] \[G_i = \langle a_i\mid a_i^2 = 1\rangle,\quad \Delta = \{a_1, \ldots, a_D\}.\]
Homework: The spectrum of \(H(D,2)\) is \[\begin{pmatrix} \theta_0 & \theta_1 & \cdots & \theta_D\\ m_0 & m_1 & \cdots & m_D\end{pmatrix},\] where \[\theta_i = D-2i \quad (0\leq i\leq D), \quad m_i = \binom{D}{i}.\]
HS MEMO
Let \(\theta \in X(G)\). Then \(\theta: X \to \{\pm 1\}\). If \[\nu(\theta) = |\{i\mid \theta(a_i) = -1\}|, \] then \(\Delta_\theta = D-2i\). Since there are \(\binom{D}{i}\) such \(\theta\), we have te assertion.
We want to compute the subconstituent algebra for \(H(D,2)\). First, we make a few observations about arbitrary graphs.
Let \(\Gamma = (X,E)\) be any graph, \(A\), the adjacemcy matrix of \(\Gamma\), and \(V\), the standard module over \(K = \mathbb{C}\).
Fix a base \(x\in X\). Write \(E_i^* = E_i^*(x)\), and \[T \equiv T(x) = \text{the algebra generated by}\; A, E_0^*, E_1^*, \ldots .\]
Definition 4.1 Let \(W\) be any irreducible \(T\)-module (\(\subseteq V\)). Then the endpoint \(r \equiv r(W)\) satisfied \[r = \min\{i\mid E_i^*W \neq 0\}.\] The diameter \(d = d(W)\) satisfied \[d = |\{i\mid E_i^*W \neq 0\}| - 1.\]
Lemma 4.1 With the above notation, let \(W\) be an irreducible \(T\)-module. Then
\((ii)\) \(AE_j^*W \subseteq E_{j-1}^*W + E_j^*W + E^*_{j+1}W\), \(0\leq j \leq d(x)\). \((E_i^*W = 0 \; \text{ if } i<j\) or \(i > d(x)\).)
\((iii)\) \(E^*_jW \neq 0\) if \(r\leq j \leq r+d\), \(=0\) if \(0\leq j\leq r\) or \(r+d < j \leq d(x)\).
\((iv)\) \(E_i^*AE^*_jW \neq 0\), if \(|i-j| = 1\) \((r \leq i,j \leq r+d)\).
Proof.
\[E_j^*\hat{y} = \begin{cases} 0 & \text{if }\; \partial(x.y)\neq j\\ \hat{y} & \text{if }\; \partial(x,y) = j.\end{cases}.\] \[\begin{align} E_i^*AE_j^*\hat{y} &= E_i^*A\hat{y} \\ & = E_i^*\sum_{z\in X, yz\in E}\hat{z}\\ & = \sum_{z\in X, yz\in E, \partial(x, z) = i}\hat{z} \tag{4.1}\\ & = 0 \; \text{ if }\; |i-j|>1 && \text{by triangle inequality.} \end{align}\] If \(|i-j| = 1\), there exist \(y, y'\in X\) such that \(\partial(x,y) = j\), \(\partial(x,y') = i\), \(yy'\in E\) by connectivity of \(\Gamma\). Hence (4.1) contains \(\widehat{y'}\) and (4.1) is not equal to zero.
\[\begin{align} AE_j^*W & = \left(\sum_{i=0}^{d(x)}E_i^*\right)AE_j^*W\\ & = E_{j-1}^*AE^*_jW + E^*_jAE_j^*W + E^*_{j+1}AE_j^*W\\ & \subseteq E^*_{j-1}W + E^*_jW + E^*_{j+1}W. \end{align}\]
\[\widetilde{W} = E^*_rW + E^*_{r+1}W + \cdots + E^*_{j-1}W.\] Observe \(0\subsetneq \widetilde{W} \subsetneq W\). Also \(A\widetilde{W} \subseteq \widetilde{W}\) by \((ii)\), and \(E_i^*\widetilde{W} \subseteq \widetilde{W}\) for every \(i\) by construction.
Thus, \(T\widetilde{W} \subseteq \widetilde{W}\), contradicting \(W\) being irreducible.