Chapter 1 Subconstituent Algebra of a Graph

Wednesday, January 20, 1993

A graph (undirected, without loops or multiple edges) is a pair $\Gamma = (X, E)$, where

$$\begin{eqnarray*} X &=& \textrm{finite set (of vertices)}\\ E &=& \textrm{set of (distinct) 2-element subsets of }X \textrm{ (= edges of ) }\Gamma. \end{eqnarray*}$$

The vertices $x$ and $y\in X$ are adjacent if and only if $xy\in E$.

Example 1.1 Let $\Gamma$ be a graph. $X = \{a, b, c, d\}$, $E = \{ab, ac, bc, bd\}$.

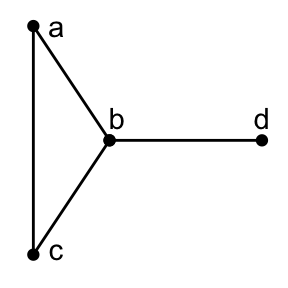
Set $n = |X|$, the order of $\Gamma$.

Pick a field $K$ ($=\mathbb{R}$ or $\mathbb{C}$). Then $\mathrm{Mat}_X(K)$ denotes the $K$ algebra of all $n\times n$ matrices with entries in $K$. (rows and columns are indexed by $X$)

Adjacency matrix $A\in \mathrm{Mat}_X(K)$ is defined by $$\begin{align} A_{xy} & = \left\{\begin{array}{cl} 1 & \textrm{ if } \; xy\in E,\\ 0 & \textrm{ else.} \end{array}\right. \end{align}$$

Example 1.2 Let $a, b, c, d$ be labels of rows and columns. Then $$A = \begin{matrix} \\ a\\ b\\c\\d\end{matrix}\begin{matrix}\begin{matrix} a & b & c & d \end{matrix}\\\begin{pmatrix} 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{pmatrix}\end{matrix}$$

The subalgebra $M$ of $\mathrm{Mat}_X(K)$ generated by $A$ is called the Bose-Mesner algebra of $\Gamma$.

Set $V = K^n$, the set of $n$-dimensional column vectors, the coordinates are indexed by $X$.

Let $\langle\; , \;\rangle$ denote the Hermitean inner product: $$\langle u, v\rangle = u^\top\cdot \bar{v} \quad (u, v\in V)$$ $V$ with $\langle\; , \;\rangle$ is the standard module of $\Gamma$.

$M$ acts on $V$: For every $x\in X$, write $$\hat{x} = \begin{pmatrix} 0 \\ \vdots \\ 0 \\ 1 \\ 0 \\ \vdots \\ 0 \end{pmatrix}\begin{matrix} \\ \\ \leftarrow x \\ \\ \\ \end{matrix}$$ where $1$ is at the $x$ position.

Then $$A\hat{x} = \sum_{y\in X, xy\in E}\hat{y}.$$ Since $A$ is a real symmetrix matrix, $$V = V_0 + V_1 + \cdots + V_r \quad \textrm{ some } r\in \mathbb{Z}^{\geq0},$$ the orthogonal direct sum of maximal $A$-eigenspaces.

Let $E_i\in\mathrm{Mat}_X(K)$ denote the orthogonal projection, $$E_i: V \longrightarrow V_i.$$ Then $E_0, \ldots, E_r$ are the primitive idempotents of $M$. $$M = \mathrm{Span}_K(E_0, \ldots, E_r),$$ $$E_iE_j = \delta_{ij}E_i \quad \textrm{for all }\; i, j, \quad E_0 + \cdots + E_r = I.$$ Let $\theta_i$ denote the eigenvalue of $A$ for $V_i$ in $\mathbb{R}$. Without loss of generality we may assume that $$\theta_0 > \theta_1 > \cdots > \theta_r.$$ Let $$m_i = \textrm{the multiplicity of }\: \theta_i = \mathrm{dim} V_i = \mathrm{rank} E_i.$$ Set $$\mathrm{Spec}(\Gamma) = \begin{pmatrix} \theta_0, & \theta_1, & \ldots, & \theta_r\\m_0, & m_1, & \ldots, & m_r\end{pmatrix}.$$ Problem. What can we say about $\Gamma$ when $\mathrm{Spec}(\Gamma)$ is given?

The following Lemma 1.1, is an example of Problem.

For every $x\in X$, $$k(x) \equiv \textrm{ valency of }x \equiv \textrm{ degree of }x \equiv |\{y\mid y\in X, \: xy\in E\}|.$$

Definition 1.1 The graph $\Gamma$ is regular of valency $k$ if $k = k(x)$ for every $x\in X$.

Lemma 1.1 With the above notation,

$(i)$ $\theta_0\leq \max\{k(x) \mid x\in X\} = k^{\max}$.
$(ii)$ If $\Gamma$ is regular of valency $k$, then $\theta_0 = k$.

Proof. $(i)$ Without loss of generality we may assume that $\theta_0>0$, else done. Let $v:=\sum_{x\in X}\alpha_x\hat{x}$ denote the eivenvector for $\theta_0$.

Pick $x\in X$ with $|\alpha_x|$ maximal. Then $|\alpha_x|\neq 0$.

Since $Av = \theta_0v$, $$\theta_0\alpha_x = \sum_{y\in X, xy\in E}\alpha_y.$$ So, $$\theta_0 |\alpha_x| = |\theta_0\alpha_x| \leq \sum_{y\in X, xy\in E}|\alpha_y| \leq k(x)|\alpha_x| \leq k^{\max}|\alpha_x|.$$

$(ii)$ All 1’s vector $v = \sum_{x\in X}\hat{x}$ satisfies $Av = kv$.

Let $x, y\in X$ and $\ell \in \mathbb{Z}^{\geq 0}$.

Definition 1.2 A path of length $\ell$ connecting $x, y$ is a sequence $$x = x_0, x_1, \ldots, x_{\ell} = y, \quad x_i\in X \quad (0\leq i\leq \ell)$$ such that $x_ix_{i+1}\in E$ for all $i$ $(0\leq i \leq \ell-1)$.

Definition 1.3 The distance $\partial(x,y)$ is the length of a shortest path connecting $x$ and $y$. $$\partial(x,y) \in \mathbb{Z}^{\geq 0} \cup \{\infty\}.$$

Definition 1.4 The graph $\Gamma$ is connected if and only if $\partial(x,y) < \infty$ for all $x, y\in X$.

From now on, assume that $\Gamma$ is connected with $|X|\geq 2$.

Set $$d_\Gamma = d = \max\{\partial(x,y)\mid x, y\in X\} \equiv \textit{the diameter of }\;\Gamma.$$

Definition 1.5 For each vertex $x\in X$, $$d(x) = \textit{the diameter with respect to }\: x = \max\{\partial(x,y)\mid y\in X\} \leq d.$$

Fix a ‘base’ vertex $x\in X$.

Observe that $$V = V_0^* + V_1^* + \cdots + V_{d(x)}^* \quad \textrm{(orthogonal direct sum)},$$ where $$V_i^* = \mathrm{Span}_K(\hat{y}\mid \partial(x,y) = i) \equiv V_i^*(x)$$ and $V_i^* = V_i^*(x)$ is called the $i$-th subconstituent with respect to $x$.

Let $E_i^* = E_i^*(x)$ denote the orthogonal projection $$E_i^*: V \longrightarrow V_i^*(x).$$ View $E_i^*(x) \in \mathrm{Mat}_X(K)$. So, $E_i^*(x)$ is diagonal with $yy$ entry: $$(E_i^*(x))_{yy} = \begin{cases} 1 & \textrm{if } \: \partial(x,y) = i,\\ 0 & \textrm{else,}\end{cases} \quad \textrm{ for } y\in X.$$ Set $$M^* = M^*(x) \equiv \textrm{Span}_K(E_0^*(x), \ldots, E_{d(x)}^*(x)).$$ Then $M^*(x)$ is a commutative subalgebra of $\mathrm{Mat}_X(K)$ and is called the dual Bose-Mesner algbara with respect to $x$.

Definition 1.6 (Subconstituent Algebra) Let $\Gamma = (X, E)$, $x$, $M$, $M^*(x)$ be as above. Let $T = T(x)$ denote the subalgebra of $\mathrm{Mat}_X(K)$ generated by $M$ and $M^*(x)$. $T$ is the subconstituent algebra of $\Gamma$ with respect to $x$.

Definition 1.7 A $T$-module is any subspace $W\subseteq V$ such that $aw\in W$ for all $a\in T$ and $w\in W$.

$T$-module $W$ is irreducible if and only if $W\neq 0$ and $W$ does not properly contain a nonzero $T$-module.

For any $a\in \mathrm{Mat}_X(K)$, let $a^*$ denbote the conjugate transpose of $a$.

Observe that $$\langle au, v\rangle = \langle u, a^*v\rangle \quad \textrm{for all }\; a\in \mathrm{Mat}_X(K), \textrm{ and for all } \; u,v\in V.$$

Lemma 1.2 Let $\Gamma = (X,E)$, $x\in X$ and $T \equiv T(x)$ be as above.

$(i)$ If $a\in T$, then $a^*\in T$.

$(ii)$ For any $T$-module $W\subset V$,

$$W^\bot := \{v\in V\mid \langle w, v\rangle = 0, \textrm{ for all }w\in W\}$$ is a $T$-module.

$(iii)$ $V$ decomposes as an orthogonal direct sum of irreducible $T$-modules.

Proof. $(i)$ It is because $T$ is generated by symmetric real matrices $$A, E^*_0(x), E^*_1(x), \ldots, E^*_{d(x)}(x).$$

$(ii)$ Pick $v\in W^\bot$ and $a\in T$, it suffices to show that $av\in W^\bot$. For all $w\in W$,

$$\langle w, av\rangle = \langle a^*w, v\rangle = 0$$ as $a^*\in T$.

$(iii)$ This is proved by the induction on the dimension of $T$-modules. If $W$ is an irreducible $T$-module of $V$, then

$$V = W + W^\bot \quad \textrm{(orthogonal direct sum)}.$$

Problem. What does the structure of the $T(x)$-module tell us about $\Gamma$?

Study those $\Gamma$ whose modules take ‘simple’ form. The $\Gamma$’s involved are highly regular.

HS MEMO

1. The subconstituent algebra $T$ is semisimple as the left regular representation of $T$ is completely reducible. See Curtis-Reiner 25.2 (Charles W. Curtis 2006).
2. The inner product $\langle a, b\rangle_T = \mathrm{tr}(a^\top\bar{b})$ is nondegenerate on $T$.
3. In general, $$\begin{align*} T\textrm{: Semisimple and Artinian} & \Leftrightarrow T\textrm{: Artinian with } J(T) = 0 \\ & \Leftarrow T\textrm{: Artinian with nonzero nilpotent element} \\ & \Leftarrow T \subset \mathrm{Mat}_X(K) \textrm{ such that for all } a\in T \textrm{ is normal.} \end{align*}$$

References

Charles W. Curtis, Irvin Reiner. 2006. Representation Theory of Finite Groups and Associative Algebras. UK. Chelsea Pub Co.