21 数理モデル(Modeling)
21.1 はじめに
データサイエンスにおいて、数理モデルを考えるとはどのようなことを意味するのでしょうか。簡単な表現は、データの(主要な)特徴の簡単な概要、またはそれを(いくつかの)数値で表現すること、と言ってもよいと思います。
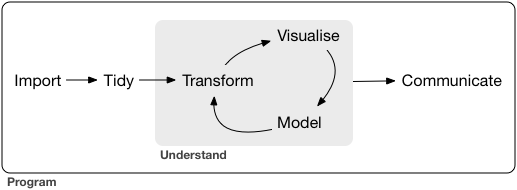
その意味では、平均値や、中央値、四分位、最大値、最小値などの、代表値と言われるものも、そうですし、正規分布など、特定の分布に近い場合に、それを定める、平均値と、標準偏差の組みも、ひとつの数理モデルを与えると言えるでしょう。
ここでは、もう少し一般的な分布に関して使われる、数理モデルについて学びます。その中でも、基本的な、二変数に関する、線形モデルについてすこし、ていねいにみていきたいと思います。
簡単にいうと、X と Y という変数があったときに、X が増えると、Y も増えるとか、減るとか、X が増加すると、Y も増加するとか、減少するとかいう傾向をみたり、それが、どの程度、直線的に、増加、減少しているかを、\(Y = b + m\cdot X\) と、直線の方程式で近似し(おおまかに表し)、それが、どの程度、実際のデータに近いかを表現する(あらわす数値をあたえる)というようなことです。
Y を X の関数で表す(X を定めると、Y を計算することができる)とも表現され、X を独立変数(independent variable)、Y を従属変数(dependent variable)と呼びます。むろん、X と Y の役割を逆にすることも可能なので、便宜的な名前です。また、統計学では、Y を目的変数(response variable)、X を説明変数(explanatory variable)と呼ぶ呼び方もされます。ただ、これらは、X によって、Y が定まるという、因果関係を表すという考え方が背景にあるのですが、傾向や関係性を見るという観点からは、これらの名前を使うことを避けたほうがよいとも言えますので、ここでは、独立変数、従属変数、説明変数、目的変数という言い方は、できるだけ避けたいと思います。
R では、\(b\)(Y 切片)は、intercept(切片)として表示され、\(m\)(直線の傾き)は、(変数 X に関する)slope(傾き)として表示されます。
R を使って、モデルについて表示される、数値の意味も説明したいと思います。数式での表現も書きますが、式を正確に覚えたりするよりも、大まかな意味を理解することを心がけてください。
数理モデルは、非常に多様なだけでなく(主要な)特徴は、分野ごとに必要度が異なることから、一般論として述べることには限界があります。H. ウィッカム(Hadley Wickham, el. al.)の R for Data Science の標準的な教科書でも、第一版には、基本的なことが含まれていましたが、第二版 には、数理モデルは含まれていません。Tidy Modeling with R を参照するようにとリンクがついています。
ここでは、オープンデータを用いたデータサイエンス、データ分析を学んでいます。基本的な線形モデルについて紹介しますが、そのモデルが適切かを判断しようとすると、t-検定や、F-検定を適用することが多いのですが、いずれも、正規分布を仮定しています。実際の社会、様々な国や、地域などを比較して検討するときに、そのデータが、正規分布をしているかどうかは、それほど簡単に判断できるわけではありません。また、これも、ある統計的な道具を使って、正規分布に近いことがある程度保証できたとしても、それに、線形モデルを適用して、どの程度適切な結果が得られるか、個人的には判断が難しいと思います。さらに、相関関係やその強さはわかっても、線形モデルなどから、因果関係を導くことはできません。個人的には、線形の関係がみてとれる、程度で、止めておくことが大切ではないかと考えています。安易に、t-検定や、F-検定を用いて、結論を導くのは、差し控えるべきで、ある結果を導くときには、ほかにも、さまざまな根拠をもつことがたいせつだと、個人的には大切だと考えます。
ということで、説明はしますが、自分は、統計がわからないから、データサイエンスはできないなどとは、言ってほしくないと思っています。統計の深い知識がなくても、データの様々な特徴を見て取ることは、可能だと思います。
21.2 準備(Setup)
library(tidyverse)
#> ── Attaching core tidyverse packages ──── tidyverse 2.0.0 ──
#> ✔ dplyr 1.1.3 ✔ readr 2.1.4
#> ✔ forcats 1.0.0 ✔ stringr 1.5.0
#> ✔ ggplot2 3.4.4 ✔ tibble 3.2.1
#> ✔ lubridate 1.9.3 ✔ tidyr 1.3.0
#> ✔ purrr 1.0.2
#> ── Conflicts ────────────────────── tidyverse_conflicts() ──
#> ✖ dplyr::filter() masks stats::filter()
#> ✖ dplyr::lag() masks stats::lag()
#> ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors
library(WDI)
library(readxl)
library(tidymodels)
#> ── Attaching packages ────────────────── tidymodels 1.1.1 ──
#> ✔ broom 1.0.5 ✔ rsample 1.2.0
#> ✔ dials 1.2.0 ✔ tune 1.1.2
#> ✔ infer 1.0.5 ✔ workflows 1.1.3
#> ✔ modeldata 1.2.0 ✔ workflowsets 1.0.1
#> ✔ parsnip 1.1.1 ✔ yardstick 1.2.0
#> ✔ recipes 1.0.8
#> ── Conflicts ───────────────────── tidymodels_conflicts() ──
#> ✖ scales::discard() masks purrr::discard()
#> ✖ dplyr::filter() masks stats::filter()
#> ✖ recipes::fixed() masks stringr::fixed()
#> ✖ dplyr::lag() masks stats::lag()
#> ✖ yardstick::spec() masks readr::spec()
#> ✖ recipes::step() masks stats::step()
#> • Use suppressPackageStartupMessages() to eliminate package startup messagesTidymodels パッケージを使いますが、これは、Tidyverse と同様に、一つのパッケージではなく、パッケージ群を表します。また、ここでは、ほんの一部しか使いませんが、一応、後々のために、インストールをし、使えるように library(tidymodels) で、読み込んでおいてください。興味のあるかたのために、Tidymodels サイトへのリンクを付けておきます。
- tidymodels: https://www.tidymodels.org
21.3 線形モデル入門
起動時に読み込まれる、datasets パッケージの、iris データを用いて、概要をみてみます。iris には、三種類の、あやめのデータが含まれていますが、ここでは、verginica と versicolor、すなわち、setosa 以外について扱います。
二つの散布図を見てみます。一つ目は、X 軸が、花弁幅(はなびらのはば)、Y 軸が、花弁長(はなびらの長さ)、二つ目は、X 軸が、萼幅(がくのはば)、Y 軸が、花弁長(がくの長さ)を表した散布図です。
df_iris0 |> ggplot(aes(Petal.Width, Petal.Length)) + geom_point()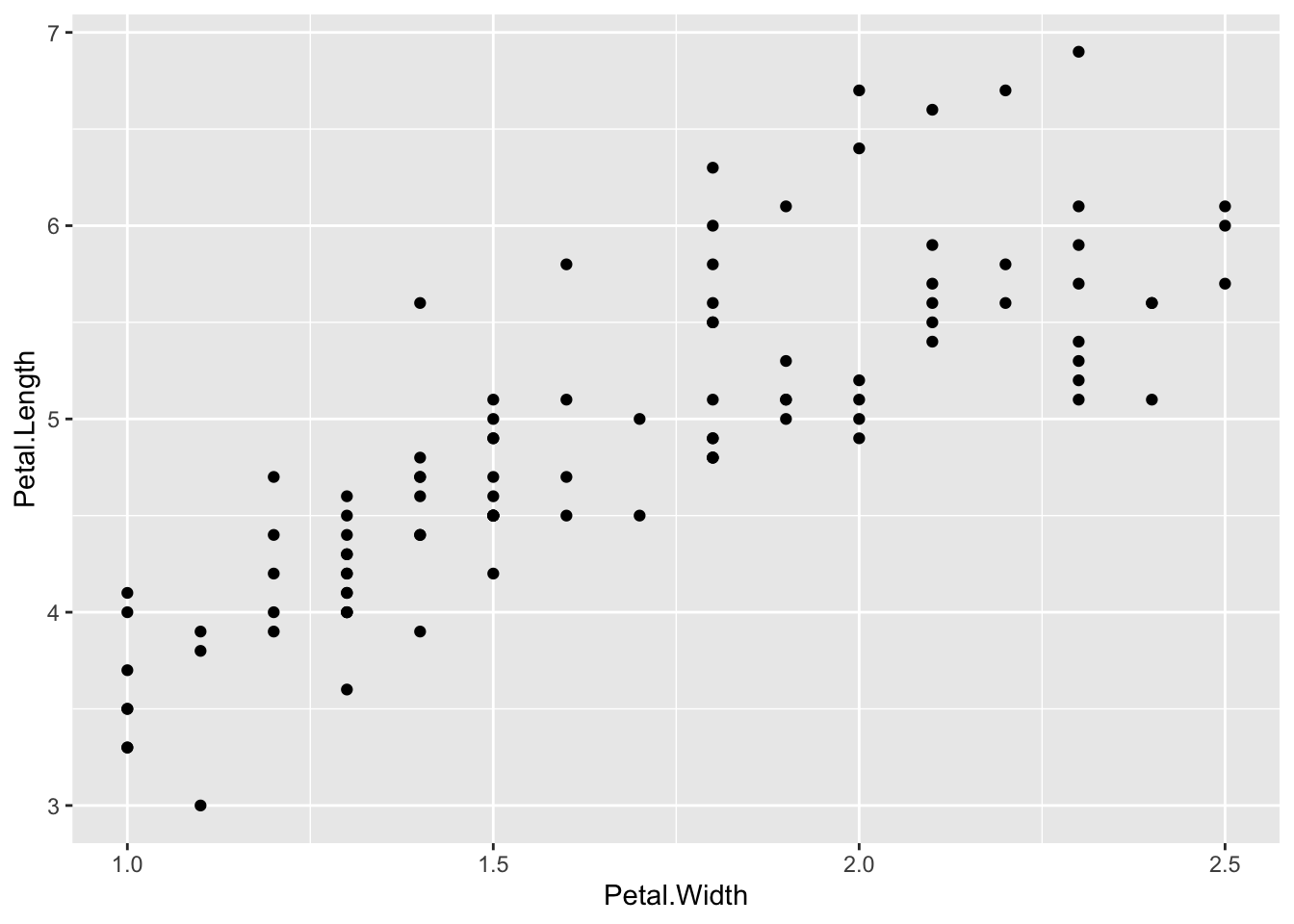
df_iris0 |> ggplot(aes(Sepal.Width, Sepal.Length)) + geom_point()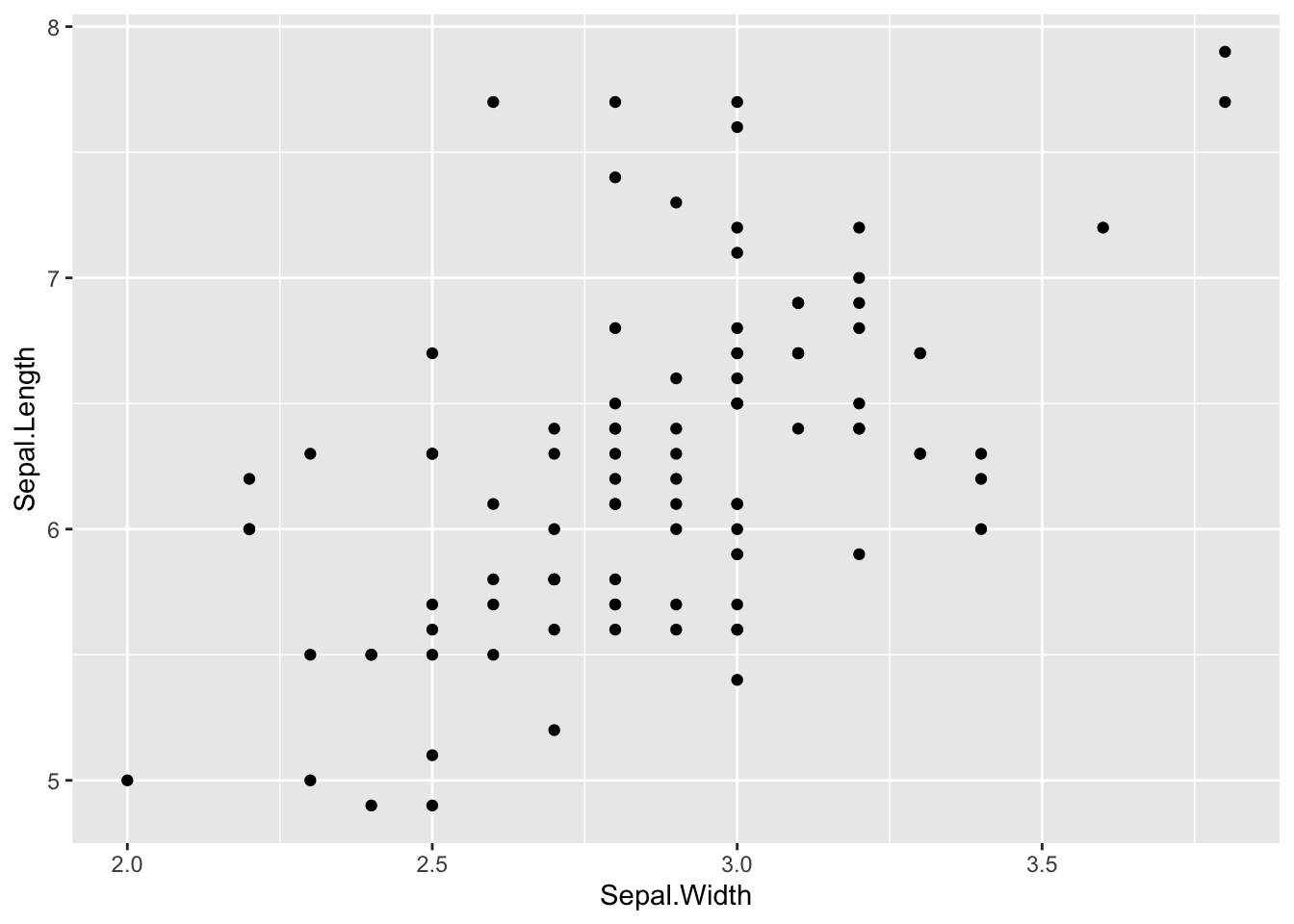
どちらも、幅(はなびらの幅や、がくの幅)が大きくなると、長さ(はなびらの長さや、がくの長さ)が大きくなる傾向があるように見えます。それは、なんとなく直感的にも自然ですよね。種類が同じ植物のはなびらや、がくの形は、だいたい同じ(相似形にちかい)と思われるからです。(直感はとてもたいせつです。直感とあわないことがあれば、立ち止まって考えて見るようにしてください。)しかし、はなびらの散布図は、それが明らかにみてとれるだけでなく、ある直線にそって(または直線的に)増加しているように見えます。がくの散布図では、その傾向が明らかではなく(ぼんやりとしていて)、直線にそって増加しているとまでは言えないように見えます。
すこし、違った、見方をする方もおられるかもしれません。定義を明確にすることで、合意ができるように、それを、数値的に表現するのが、線形モデルを使った表現です。まずは、それぞれに、増加傾向をあらわす直線を描いてみましょう。これは、ある一定の方法で描いたもので、歴史的背景から、回帰直線(regression line)と呼ばれすが、いまは、大体、そんなものだと考えてくださって構いません。
df_iris0 |> ggplot(aes(Petal.Width, Petal.Length)) + geom_point() + geom_smooth(method="lm",formula=y~x, se=FALSE)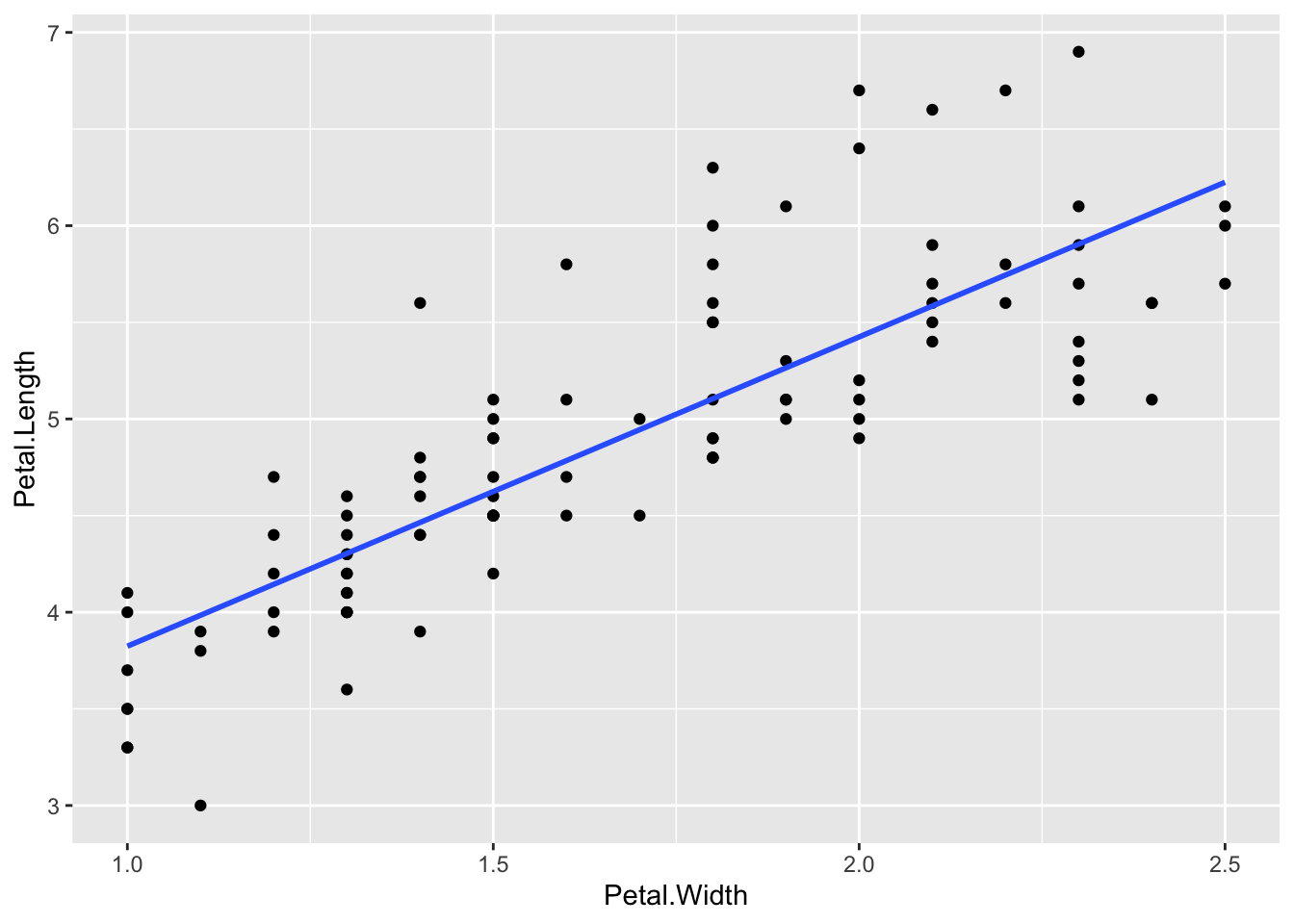
df_iris0 |> ggplot(aes(Sepal.Width, Sepal.Length)) + geom_point() + geom_smooth(method="lm",formula=y~x, se=FALSE)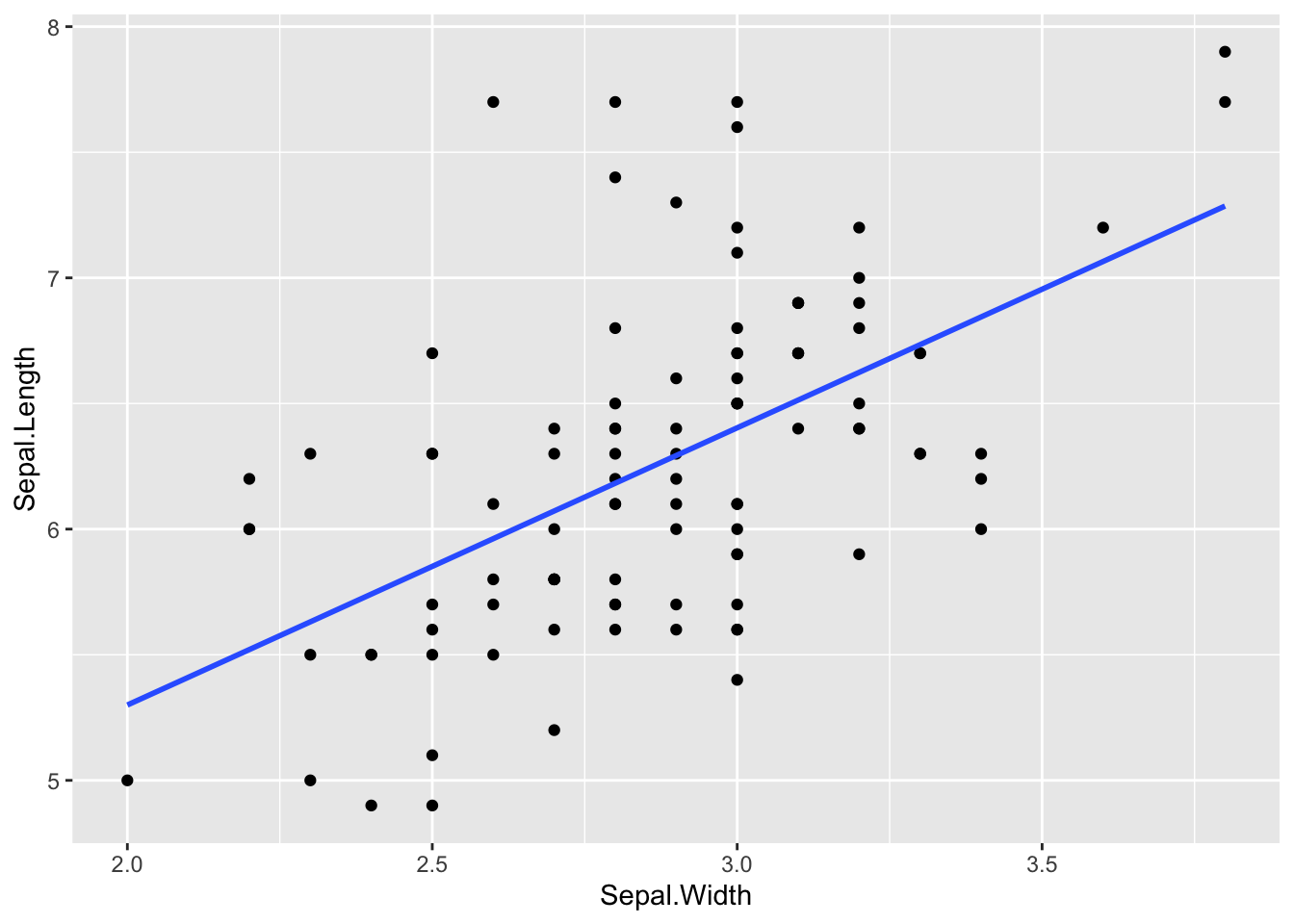
たしかに、この二つの散布図と、直線を見ると、それぞれ(はなびらや、がくの)幅が増加すると長さも増加する傾向にあるようです。そこで、今度は、直線に近い、増加傾向にあると仮定して、適切な直線の方程式を求めてみます。それは、次のようにして求めることができます。
21.3.1 線形モデルの例(Linear Models by Examples)
21.3.1.1 Linear Model: Petal.Length ~ Petal.Width
はなびらの長さを、はなびらの幅を変数とする、直線の方程式で近似してみます。
df_iris0 |> lm(Petal.Length ~ Petal.Width, data = _)
#>
#> Call:
#> lm(formula = Petal.Length ~ Petal.Width, data = df_iris0)
#>
#> Coefficients:
#> (Intercept) Petal.Width
#> 2.224 1.600Call の部分は、「このような(X を Petal.Width として、Y を Petal.Length の一次式、すなわち、\(Y = b + m\cdot X\) と表わそうと)線形モデルで考えると」といった、意味です。
Coefficients は、係数の意味です。次に、(Intercept) が、2.224、Petal.Width が 1.600 とありますから、1.600 が 一次式で表したときの Petal.Width の係数で、式で書くと次のようになります。
Formula: \(\text{Petal.Length} = 2.224 + 1.600\cdot \text{Petal.Width}\)
Petal.Width の範囲が限られていますから、Y 切片は確認できませんが、だいたい見当が付きますし、傾きは、X が 1 大きくなると、Y がどれぐらい大きくなるかという数ですから、だいたい、見当がつきますね。
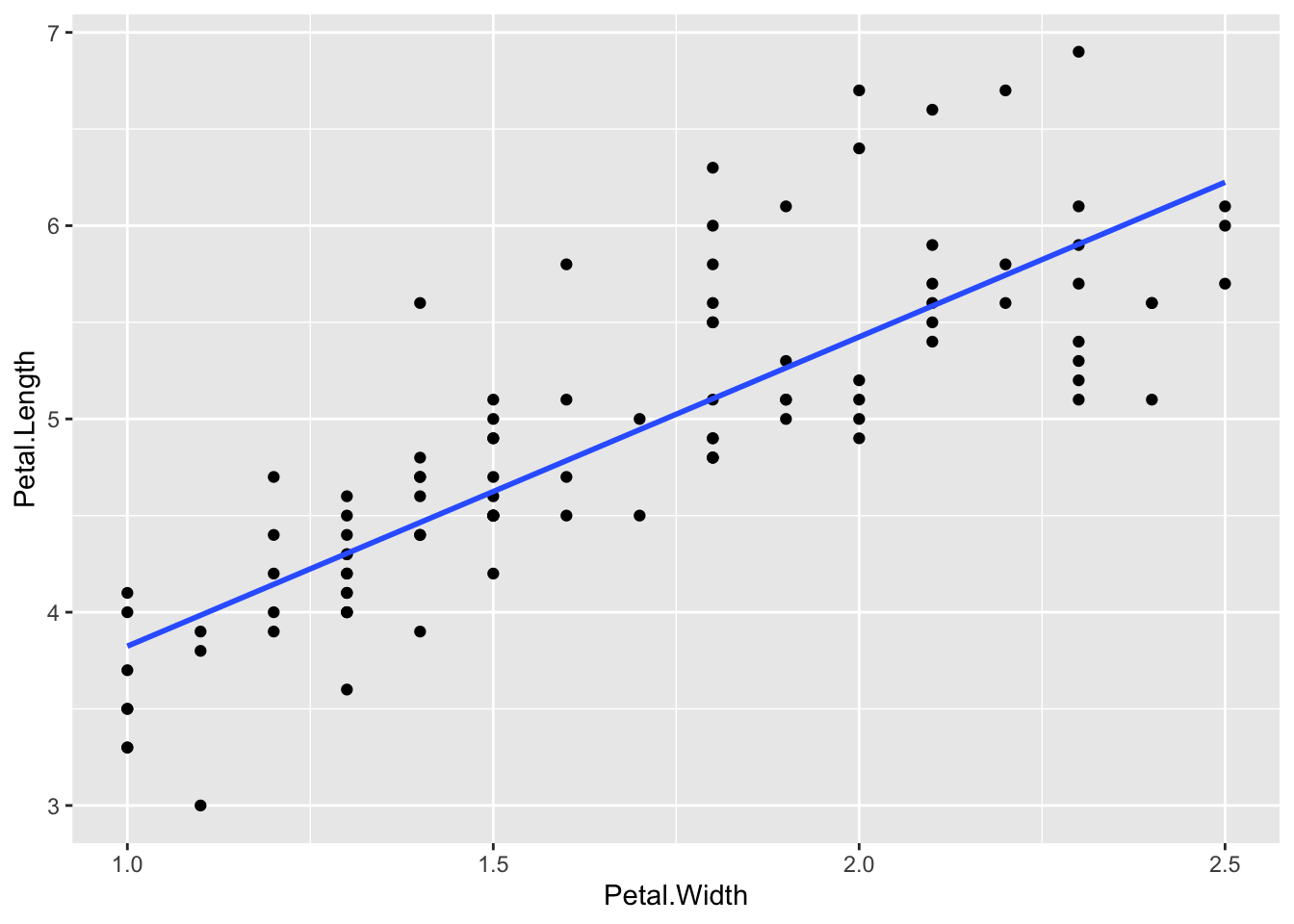
21.3.1.2 Linear Model: Sepal.Length ~ Sepal.Width
がくの長さを、がくの幅を変数とする、直線の方程式で近似してみます。
df_iris0 |> lm(Sepal.Length ~ Sepal.Width, data = _)
#>
#> Call:
#> lm(formula = Sepal.Length ~ Sepal.Width, data = df_iris0)
#>
#> Coefficients:
#> (Intercept) Sepal.Width
#> 3.093 1.103式は、次のようになっていることがわかります。
Formula: \(\text{Sepal.Length} = 3.093 + 1.103\cdot \text{Sepal.Width}\)
下のグラフから、だいたいの、Y 切片や、傾きを読み取って、上の式と比較してください。
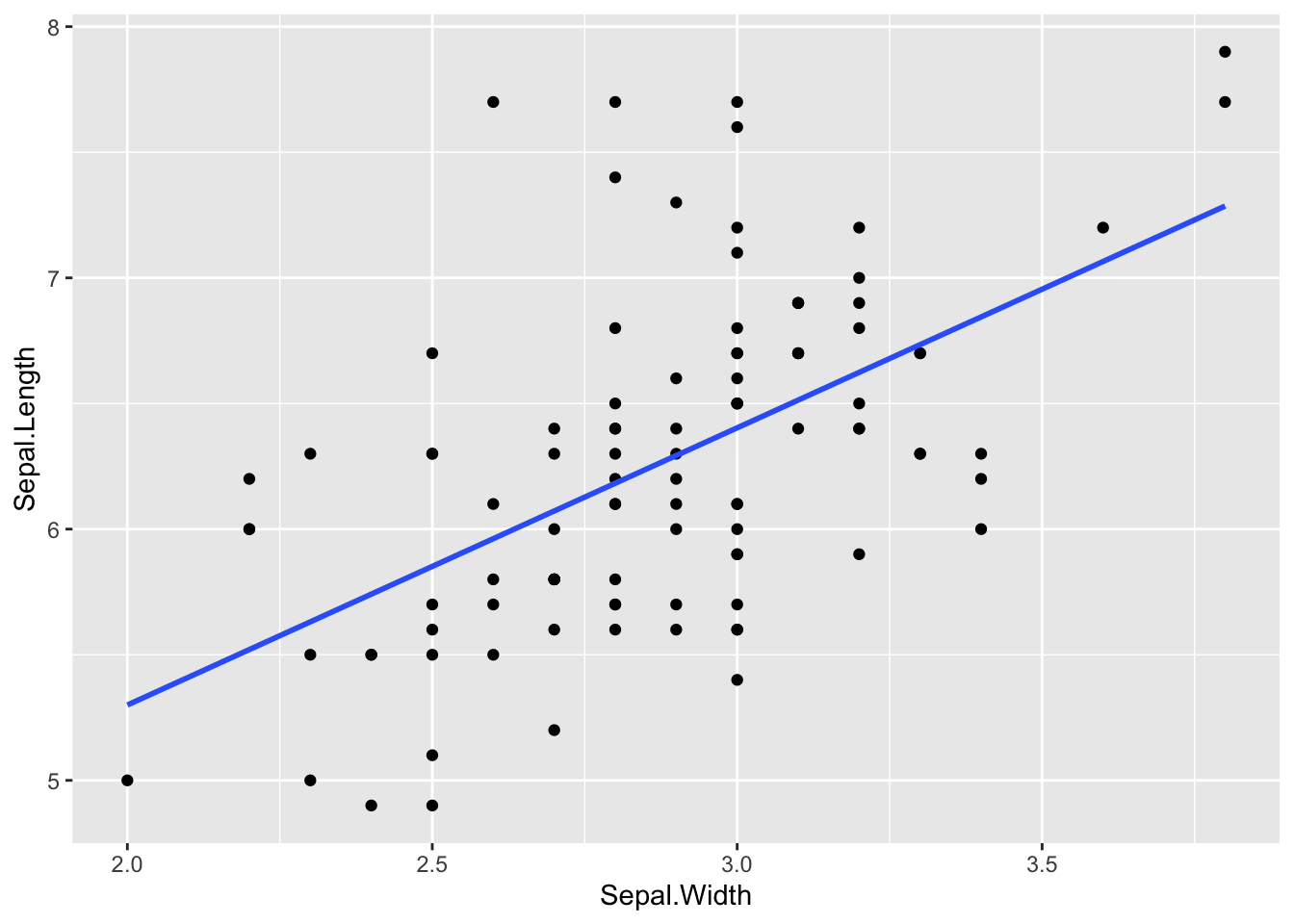
21.3.1.3 決定係数(R squared)
日本語では、決定係数と呼ばれることが多いようですが、R squared の意味を簡単に説明します。
まず、決定係数(R squared)は、0 と 1 の間の値を取ります。モデルの当てはまり具合を表す数とも表現されます。
The coefficient of determination R2 represents the strength of fit of the model.
このモデル(現在の場合は X の関数として、Y の値をおおまかに表現する線形モデル)によって、どのていど、実際の値が決まるかをあらわす一つの指標です。この値が、1 のときは、ピッタリ合致していることを意味し、0 のときは、X の値に依存しない、平均値と、変わらないという意味です。たとえば、はなびらモデルでは、下のようになりますから、68% 程度決定する、または、適合するという言い方をします。がくモデルの場合には、31% 程度決定する、または、適合するという言い方をします。はなびらモデルのほうが、がくモデルよりもより直線的といいうことを表す数ということになります。
(Multiple) R Squared: a value between 0 and 1, the model’s strength. It is a measurement of the model quality. If the value is close to 1, the model quality is high. If it is close to 0, the model quality is low.
Petal.Length ~ Petal.Width: R squared = 0.6779 - 68%
df_iris0 |> lm(Petal.Length ~ Petal.Width, data = _) |> summary()
#>
#> Call:
#> lm(formula = Petal.Length ~ Petal.Width, data = df_iris0)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -0.9842 -0.3043 -0.1043 0.2407 1.2755
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 2.2240 0.1926 11.55 <2e-16 ***
#> Petal.Width 1.6003 0.1114 14.36 <2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.4709 on 98 degrees of freedom
#> Multiple R-squared: 0.6779, Adjusted R-squared: 0.6746
#> F-statistic: 206.3 on 1 and 98 DF, p-value: < 2.2e-16Sepal.Length ~ Sepal.Width: R squared = 0.3068 - 31%
df_iris0 |> lm(Sepal.Length ~ Sepal.Width, data =_) |> summary()
#>
#> Call:
#> lm(formula = Sepal.Length ~ Sepal.Width, data = df_iris0)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -1.0032 -0.3877 -0.0774 0.3200 1.7381
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 3.0934 0.4844 6.387 5.70e-09 ***
#> Sepal.Width 1.1033 0.1675 6.585 2.27e-09 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.5547 on 98 degrees of freedom
#> Multiple R-squared: 0.3068, Adjusted R-squared: 0.2997
#> F-statistic: 43.36 on 1 and 98 DF, p-value: 2.27e-09上のように、summary() 関数をつかうと、Multiple R-squared や、Adjusted R-squared と R squared 値は、出てきますが、現在の場合は、Multiple R-squared が、決定係数だと考えてください。
いまは、Y を、X の関数として表しましたが、X ではなく、X1、X2、などとたくさんの変数を使って、表し、全体のデータ(観測値)の個数が、あまり多くないときは、Multiple R-squared よりも、Adjusted R-squared のほうが、より適切になってくるばあいはあるので、このように、2つの数が書かれています。
また、決定係数(R squared)は、線形モデル以外にも使えますので、モデルの適合性を表す、たいせつな指標のひとつと理解しておいてください。
summary() には、他にもたくさんの、値が出ています。あとで、それぞれについて、簡単に見ていきたいと思います。
決定係数が1に近いと良い(強い)モデルで、0に近いと悪い(弱い)モデルということになりますが、どの程度ならば、良いモデルかは一概に言えません。分野にもよりますが、0.3 より小さければ、あまりよいモデルだとは言えず、0.7 より大きければ、よいモデルのひとつだと考えても良いのではないかと思います。
上の2つのモデルは、微妙ですが、花びらモデルのほうが、良い(より適合した)モデルだと表現できます。
21.3.2 線形モデルの基礎(Linear Model Basics): y ~ x
R では、線形モデルを次のように定めます。y~x は、x の関数で、y を表すという意味です。パイプを使うときは、その下の式のようになります。パイプは原則として、最初の変数として、一つ前の出力が読み込まれますが、lm(arg1, arg2) の場合には、arg2 2つ目の変数が、データですから、それを表すために、data = _ (または、%>% の場合には、そこに、ピリオッド(半角))を書き、そのことを示します。場所指定の ‘_’ (または ‘.’) (place holder) と言います。
lm(y~x, data)data |> lm(y~x, data=_) # data = をつけないとエラーになりますdata %>% lm(y~x, .)y 切片や、傾きが得られます。(y-intercept, and slope: rate of increase or decrease)
モデルのより詳細な情報は、summry() によって得ることができます。パイプを使う場合には、その次のコードとなります。
summary(lm(y~x, data))data |> lm(y~x, .) |> summary()具体的な例から、それぞれの数値がなにを表しているのか見ていきましょう。
df1 <- data.frame(x = c(1,2,3,4), y = c(1,0.5,2, 1.5))
ybar <- mean(df1$y)
mod1 <- lm(y~x, df1)
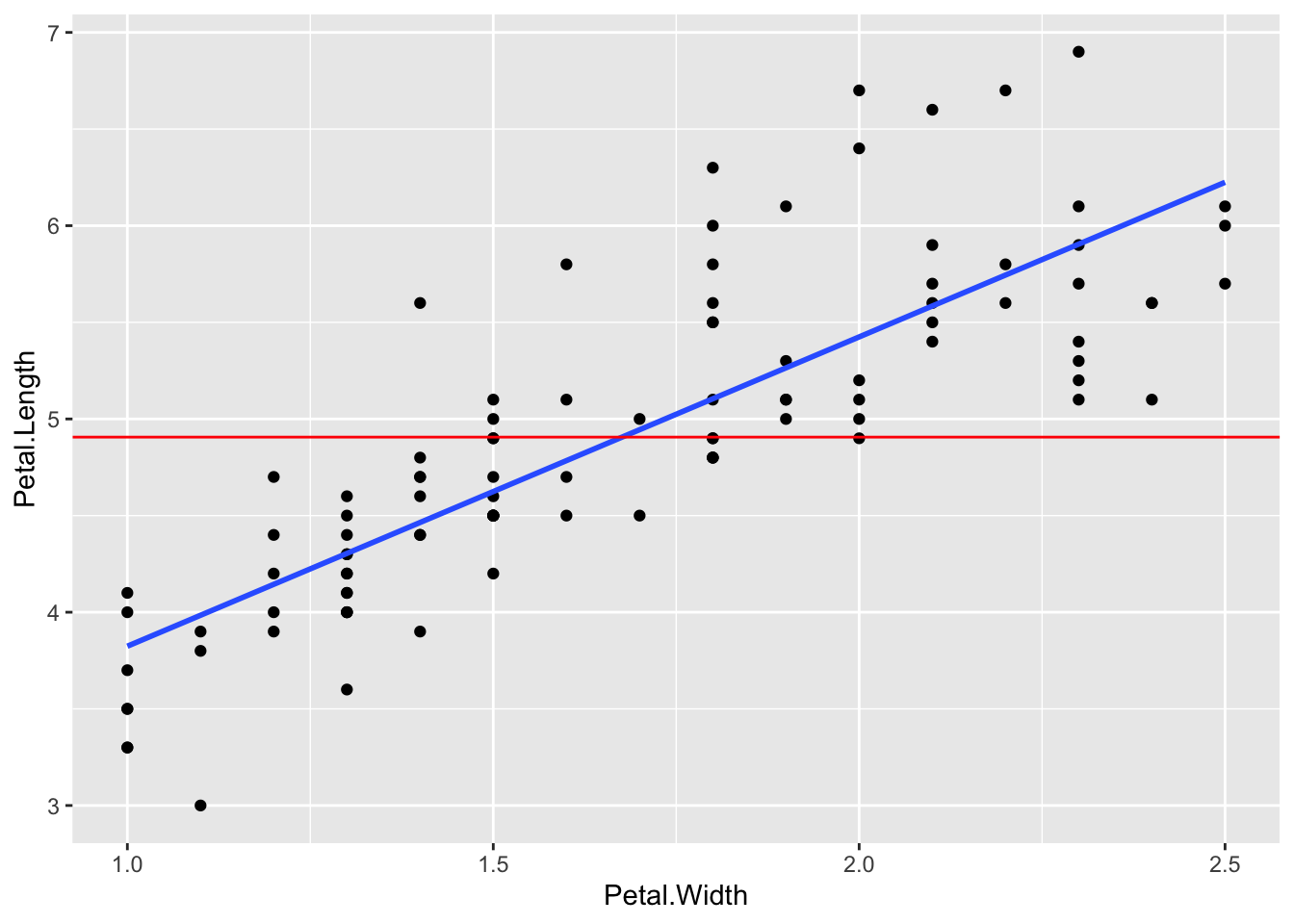
augment(mod1) |> ggplot() + geom_point(aes(x,y)) + geom_smooth(aes(x,y), formula = y~x, method = "lm", se = FALSE) + geom_hline(yintercept = ybar, linetype="longdash", col = "red") + geom_point(aes(x, ybar), shape=4) + geom_point(aes(x, .fitted), shape =9, size=2) + geom_text(aes(x, ybar, label = paste0("(",x,",",1.25,")")), nudge_y = -0.1, col = "red") + geom_text(aes(x, .fitted, label = paste0("(",x,",",.fitted,")")), nudge_y = -0.1, col = "blue") + geom_text(aes(x, y, label = paste0("(",x,",",y,")")), nudge_y = -0.1) - \((x_1, y_1)\), \((x_2,y_2)\), \((x_3, y_3)\), \((x_4, y_4)\): Data points - データの4つの点をあらわす黒点
- \(\bar{y}\): mean of y = \((y_1 + y_2 + y_3 + y_4)/4\). (相加)平均値を表す赤線
-
\(\hat{y}_i\): prediction at \(x_i\), 線形モデルの一次式で与えられる値
- \((x_1, \hat{y}_1)\), \((x_2, \hat{y}_2)\), \((x_3, \hat{y}_3)\), \((x_4, \hat{y}_4)\) are on the regression line. 回帰直線上の◇で表された点
- \(y_1-\hat{y}_1\), \(y_2-\hat{y}_2\), \(y_2-\hat{y}_2\), \(y_2-\hat{y}_2\) are called residues. 実際の値から、モデルでの予測値を引いたもので、残差と呼ばれます
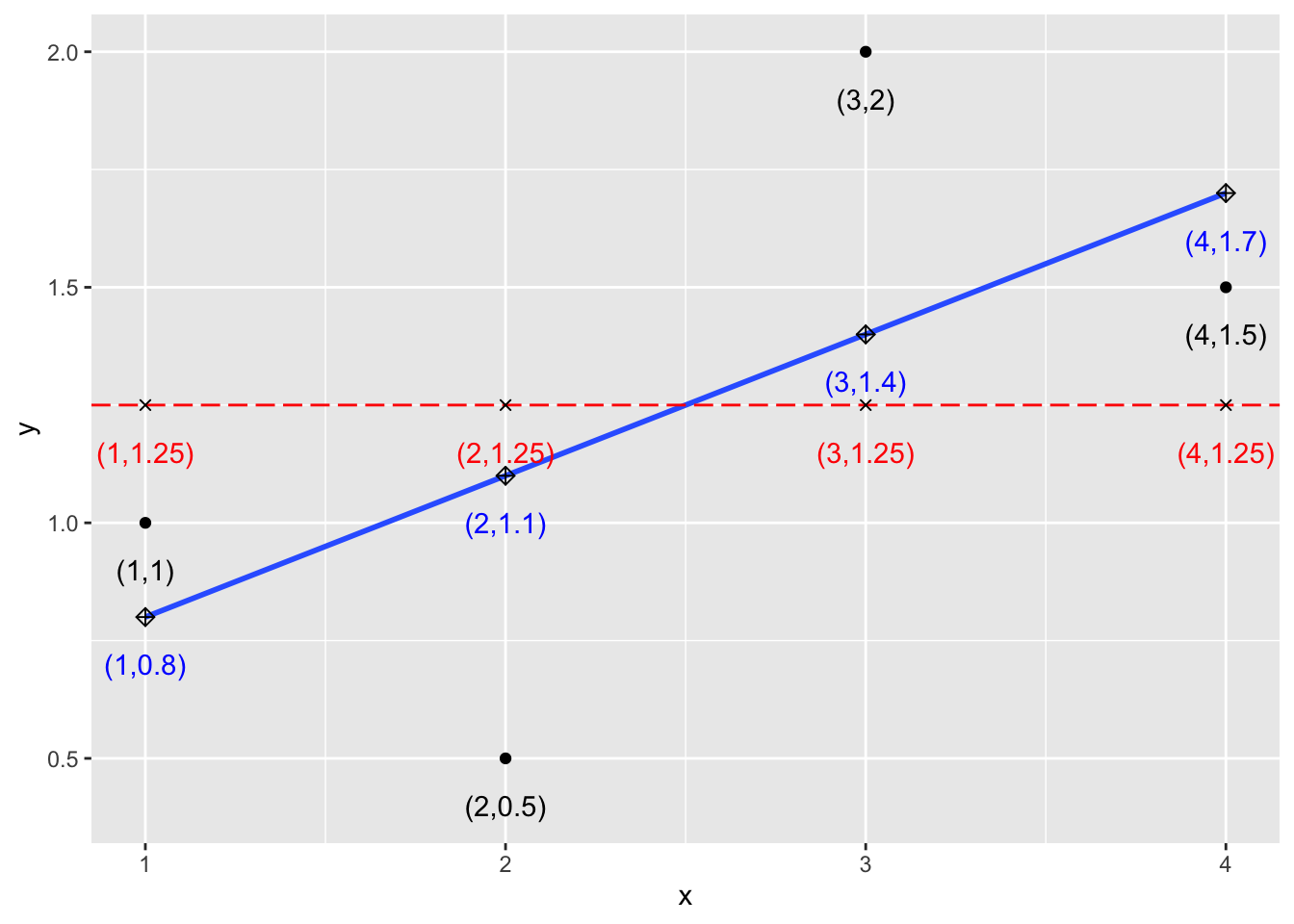
線形モデルの一次式で与えられる値(fitted values)は次のようにしても表示できます。
mod1$fitted.values
#> 1 2 3 4
#> 0.8 1.1 1.4 1.721.3.2.1 決定係数(R Squared)
\(SS_{tot}\) は、実際の値から平均値を引いたものを、二乗して足したものです。二乗してあるので、かならず正(正確には非負)になります。
\(SS_{res}\) は、実際の値から(この線形)モデルによって予測したあたいを引いたものを、二乗して足したものです。二乗してあるので、かならず正(正確には非負)になります。
\(R^2\) は、一番下の式で定義されます。完全に予測が実際の値と一致していると、\(SS_{res}\) は、0 になりますから、その場合は、商の分子が 0 で、\(R^2\) の値は、1 になります。
線形モデルの、直線の方程式は、直線の中で、\(SS_{res}\) が一番小さくなるものを(最小二乗法という方法で)選んであり、平均を通る直線をから計算したものよりは、小さくなるので、商の部分は、1 以下、すなわち、\(R^2\) の値は、0 以上 1 以下となります。
\[SS_{tot} = (1-1.25)^2 + (0.5-1.25)^2 + (2-1.25)^2 + (1.5-1.25)^2 = 1.25\] \[SS_{res} = (1-0.8)^2 + (0.5-1.1)^2 + (2-1.4)^2 + (1.5-1.7)^2 = 0.8\] \[R^2 = 1 - \frac{SS_{res}}{SS_{tot}} = 1- \frac{0.8}{1.25} = 0.36.\]
実際に、mod1 の summary() から値を取り出す方法をいくつか書いておきます。glance は、tidymodel に含まれる、パッケージ broom の関数で、モデルの概要(summary)を、表(この場合は、tidyverse の標準の tibble)として出力するものです。
summary(mod1)$r.squared
#> [1] 0.36
mod1 |> summary() |> glance()
mod1 |> glance() |> pull(r.squared)
#> [1] 0.36
mod1 |> glance() |> select(`R Squared` = r.squared)21.3.3 モデル概要
一般的な場合に、それぞれの数値を表す数式(Mathematical Formula)と簡単な説明を記します。
- \(x = c(x_1, x_2, \ldots, x_n)\) : X 変数(the X (independent) variable) 例 Petal.Width
- \(y = c(y_1, y_2, \ldots, y_n)\) :Y 変数(the Y (dependent) variable) 例 Petal.Length
- \(\mbox{pred} = c(\hat{y}_1, \hat{y}_2, \ldots, \hat{y}_n)\) :モデル予測値(the predicted values by a (linear regression) model)例 \(\hat{y}_i = b + m\cdot x_i\)
例は、はなびらモデルを使って説明します。
df_iris0 |> lm(Petal.Length ~ Petal.Width, data = _) %>% summary()
#>
#> Call:
#> lm(formula = Petal.Length ~ Petal.Width, data = df_iris0)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -0.9842 -0.3043 -0.1043 0.2407 1.2755
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 2.2240 0.1926 11.55 <2e-16 ***
#> Petal.Width 1.6003 0.1114 14.36 <2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.4709 on 98 degrees of freedom
#> Multiple R-squared: 0.6779, Adjusted R-squared: 0.6746
#> F-statistic: 206.3 on 1 and 98 DF, p-value: < 2.2e-1621.3.3.2 Residuals(残差)
残差は、実際の値から、予測値を差し引いた値(Difference between what the model predicted and the actual value of y):\(e_i = y_i - \hat{y}_i\)
その、分布の、最小値、第一四分位、中央値、第三四分位、最大値が表示されています。次のようにしても、表示できます。
Tidymodels に含まれる、broom パッケージの augument() 関数を使うと、予測値 predicted values (pred) または、fitted values は、.fitted 列に、残差 residues は、.resid に追加されます。(他の列については、さしあたって不要ですが、Help などを参照してください。)
df_iris0 |> lm(Petal.Length ~ Petal.Width, data = _) |> augment()したがってそれを使えば、Residuals の部分の値は、次のようにして得られます。
21.3.3.3 数式による定義
\[ \begin{aligned} \mbox{$x$ の平均:} mean(x) & = \frac{1}{n}\sum_i x_i \\ \mbox{$y$ の平均:} mean(y) & = \frac{1}{n}\sum_i y_i \\ \mbox{$x$ の分散:} var(x) & = \frac{1}{n}\sum_i(x_i-mean(x))^2 \\ \mbox{$y$ の分散:} var(y) & = \frac{1}{n}\sum_i(y_i-mean(y))^2 \\ \mbox{$x$ と $y$ の共分散:} cov(x) & = \frac{1}{n}\sum_i(x_i-mean(x))(y_i-mean(y)) \\ \mbox{$x$ と $y$ の相関係数:} cor(x) & = \frac{cov(x,y)}{\sqrt{var(x)}\sqrt{var(y)}}\\ \mbox{回帰直線の係数: slope} &= \frac{cov(x,y)}{var(x)} = \frac{cor(x,y)\sqrt{var(y)}}{\sqrt{var(x)}}\\ \mbox{全平方和 total sum of squares:} &SS_{tot} = \sum_{i}(y_i-mean(y))^2\\ \mbox{残差平方和 residual sum of squares:} &SS_{res} = \sum_{i}(y_i-\mbox{pred}_i)^2 \\ &= \sum_{i}(y_i-\hat{y}_i)^2\\ \mbox{決定係数 R squared:} R^2 & = 1 - \frac{SS_{res}}{SS_{tot}} = cor(x,y)^2 \end{aligned} \]
21.3.3.4 Adjusted R Squared(自由度修正済み決定係数)
\[\text{Adjusted }R^2 = 1- \frac{(1-R^2)(n-1)}{n-k-1}\] \(n\): 行数(観測値の数)number of observations, the number of rows
\(k\): number of variables used for prediction
21.3.3.5 Coefficients(係数)
Tidymodels に含まれる、broom パッケージの tody() 関数を使うと、係数の部分を表として取り出すことができます。
df_iris0 |> lm(Petal.Length ~ Petal.Width, data = _) |> tidy()ここに現れる、statistics は t-検定の、値で、p.value が最初に定めた値、たとえば、0.05よりも、小さければ、Intercept や、Petal.Width の係数が、0 である確率は非常に小さいといいます。
21.3.3.6 Other Model Summaries(その他のモデル概要)
Tidymodels に含まれる、broom パッケージの glance() 関数を使うと、残りの値が表示できます。
df_iris0 |> lm(Petal.Length ~ Petal.Width, data = _) |> glance()r.squared は、R squared(決定係数)、adj.r.squared は、Adjusted R Squared(自由度修正済み決定係数)、sigma は、Residual Standard Error(残差標準誤差)、statistic は、f 検定の F value(F 値)、p.value は、F 分布の p値です。
最初の2つはすでに説明しました。
\[ \mbox{statistic} = \frac{SS_{tot} - SS_{res}}{SS_{res}}\cdot \frac{n-(k+1)}{k} \]
p値が、定めた値、例えば、0.05 より小さいと、2つの変数が、関係しない確率が非常に小さいということになります。
Correlation Constant (相関係数)
式に現れるように、\(R^2 = cor(x,y)^2\) でしたから、相関係数が分かれば、この場合の決定係数はわかることになります。特に、相関係数の大きな変数の対を見つければ、それから計算する、線形モデルは、強いモデルだということになります。
df_iris0 |> select(1:4) |> cor()
#> Sepal.Length Sepal.Width Petal.Length
#> Sepal.Length 1.0000000 0.5538548 0.8284787
#> Sepal.Width 0.5538548 1.0000000 0.5198023
#> Petal.Length 0.8284787 0.5198023 1.0000000
#> Petal.Width 0.5937094 0.5662025 0.8233476
#> Petal.Width
#> Sepal.Length 0.5937094
#> Sepal.Width 0.5662025
#> Petal.Length 0.8233476
#> Petal.Width 1.0000000その自乗を計算することもできます。
この例では、Sepal.Length と、Petal.Length の相関が最も強いことがわかります。
select(1:4) で、最初の四列を取り出していますが、iris のデータは、五つの変数(五列)で五番目は、Species(種類)でしたから、Species の列以外という意味です。すこで、下では、select(-5) としています。どちらでも同じです。Species は、文字列で種類が書かれていましたから、相関係数を求めようとすると、エラーになります。
cormat <- df_iris0 |> select(1:4) |> cor()
cormat*cormat
#> Sepal.Length Sepal.Width Petal.Length
#> Sepal.Length 1.0000000 0.3067552 0.6863769
#> Sepal.Width 0.3067552 1.0000000 0.2701944
#> Petal.Length 0.6863769 0.2701944 1.0000000
#> Petal.Width 0.3524909 0.3205853 0.6779013
#> Petal.Width
#> Sepal.Length 0.3524909
#> Sepal.Width 0.3205853
#> Petal.Length 0.6779013
#> Petal.Width 1.0000000
df_iris <- datasets::iris
as_tibble(df_iris) |> filter(Species == "setosa") |> select(-5) %>% cor()
#> Sepal.Length Sepal.Width Petal.Length
#> Sepal.Length 1.0000000 0.7425467 0.2671758
#> Sepal.Width 0.7425467 1.0000000 0.1777000
#> Petal.Length 0.2671758 0.1777000 1.0000000
#> Petal.Width 0.2780984 0.2327520 0.3316300
#> Petal.Width
#> Sepal.Length 0.2780984
#> Sepal.Width 0.2327520
#> Petal.Length 0.3316300
#> Petal.Width 1.0000000
as_tibble(df_iris) |> filter(Species == "virginica") |> select(-5) |> cor()
#> Sepal.Length Sepal.Width Petal.Length
#> Sepal.Length 1.0000000 0.4572278 0.8642247
#> Sepal.Width 0.4572278 1.0000000 0.4010446
#> Petal.Length 0.8642247 0.4010446 1.0000000
#> Petal.Width 0.2811077 0.5377280 0.3221082
#> Petal.Width
#> Sepal.Length 0.2811077
#> Sepal.Width 0.5377280
#> Petal.Length 0.3221082
#> Petal.Width 1.0000000
as_tibble(df_iris) |> filter(Species == "versicolor") |> select(-5) |> cor()
#> Sepal.Length Sepal.Width Petal.Length
#> Sepal.Length 1.0000000 0.5259107 0.7540490
#> Sepal.Width 0.5259107 1.0000000 0.5605221
#> Petal.Length 0.7540490 0.5605221 1.0000000
#> Petal.Width 0.5464611 0.6639987 0.7866681
#> Petal.Width
#> Sepal.Length 0.5464611
#> Sepal.Width 0.6639987
#> Petal.Length 0.7866681
#> Petal.Width 1.0000000
as_tibble(df_iris) |> filter(Species == "virginica") |> ggplot(aes(Sepal.Length, Petal.Length)) + geom_point() + geom_smooth(method = "lm", formula = y~x, se = FALSE)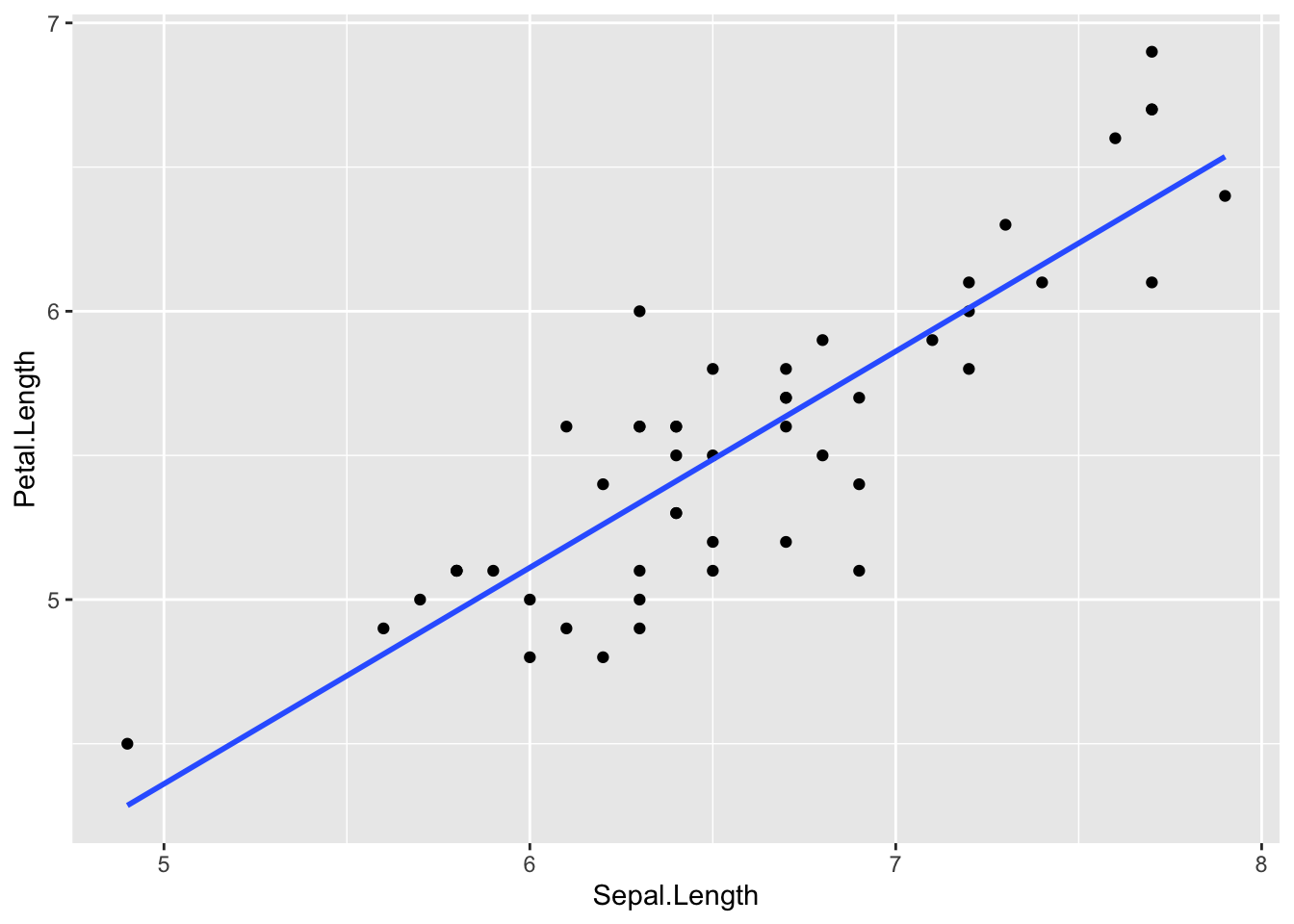
as_tibble(df_iris) |> filter(Species == "virginica") |> lm(Petal.Length ~ Sepal.Length, data = _) |> glance() |> pull(r.squared) |> sqrt()
#> [1] 0.86422472つの変数の場合には、このように、相関係数を見てみることも、大切です。Correlations of the data suggest the possible strength of linear model y ~ x.
df_iris |> select(-5) |> cor()
#> Sepal.Length Sepal.Width Petal.Length
#> Sepal.Length 1.0000000 -0.1175698 0.8717538
#> Sepal.Width -0.1175698 1.0000000 -0.4284401
#> Petal.Length 0.8717538 -0.4284401 1.0000000
#> Petal.Width 0.8179411 -0.3661259 0.9628654
#> Petal.Width
#> Sepal.Length 0.8179411
#> Sepal.Width -0.3661259
#> Petal.Length 0.9628654
#> Petal.Width 1.0000000最後に、もう一つ、iris の例を描いておきます。
df_iris |> ggplot(aes(Sepal.Width, Sepal.Length)) +
geom_point(aes(color = Species)) +
geom_smooth(aes(color = Species), formula = "y~x", method = "lm", se = FALSE) +
geom_smooth(formula = "y~x", method = "lm", se = FALSE, color = "black", linetype = "dotted")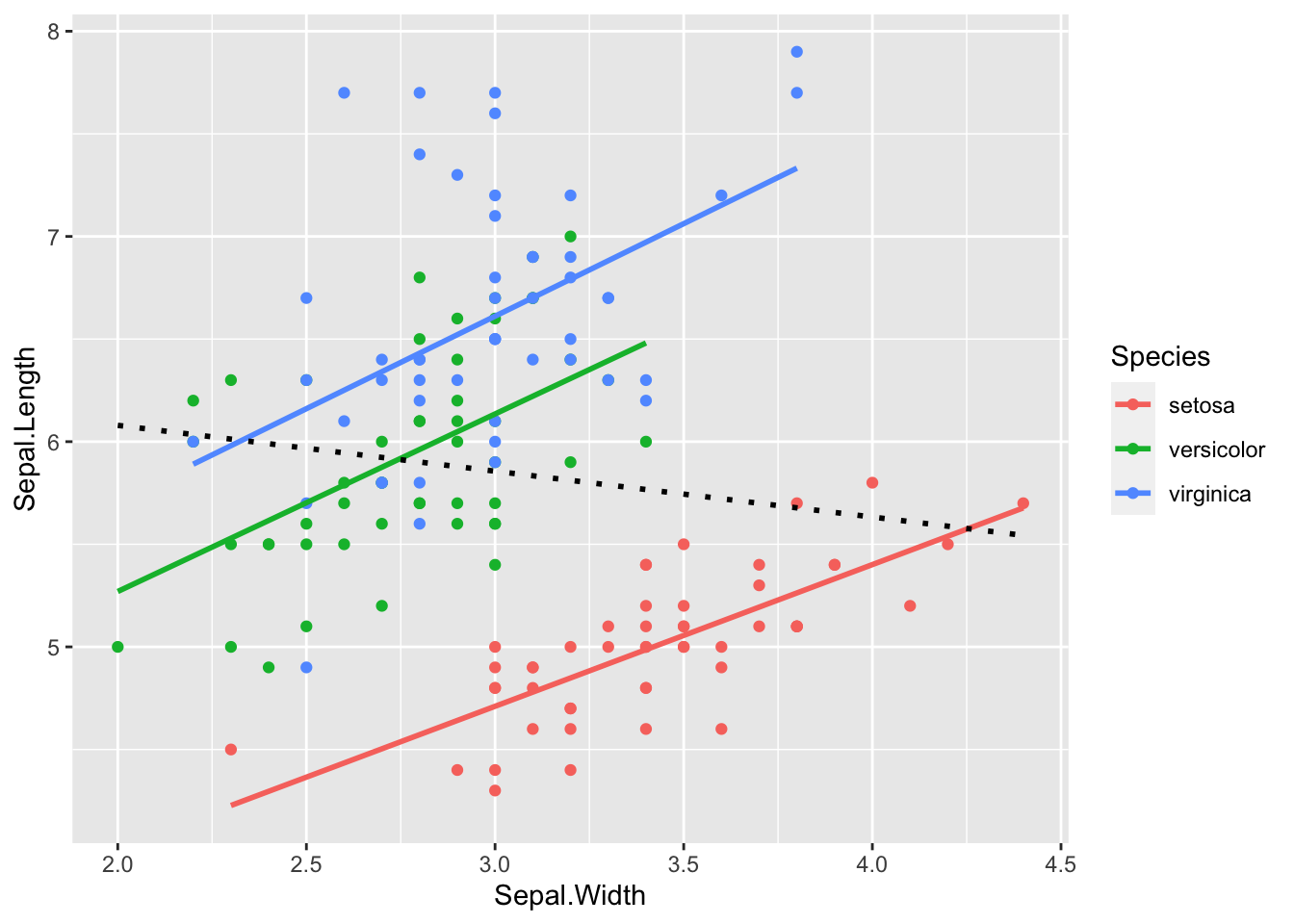
点線は、全体の、がくモデルについての、回帰直線です。どのようなことがわかりますか。
三つの種別ごとで見ると、回帰直線は、右肩上がり、すなわち、萼(がく)幅が大きくなると、萼長が大きくなっている。
全体で見ると、回帰直線は、右肩下がり、すなわち、萼(がく)幅が大きくなると、萼長が小さくなっている。
最初に、同じ種類のあやめ(iris)では、おそらく、萼の形などは相似(似た形をしている)だろうから、「萼(がく)幅が大きくなると、萼長が大きくなっていると予想される」と書きました。しかし、上のグラフからみると、これら三種類のあやめ全体ではそうなっておらず、三種類個別にみると、予想のようになっていることがわかります。
この場合、Species が交絡因子(confounder)になっていると言います。
21.3.3.7 ChatGPT への質問と回答
Q. 交絡因子、confounder について、説明してください。
iris の data で、Sepal.Width と Sepal.Length でみると、負の相関になっている、または、回帰直線の傾きが負になっているが、各 Species ごとにみると、傾きが正になっている。この場合も、Species が交絡因子になっていると言えますか。
ChatGPT (2023.9.19)
交絡因子(confounder)は、2つ以上の変数間の関係を誤解させる要因であり、研究結果に偏りをもたらす可能性がある変数です。交絡因子は、主な関心事(たとえば、Sepal.WidthとSepal.Lengthの関係)と関係がある可能性があり、その関係を調べる際に考慮する必要があります。
IrisデータセットでSepal.WidthとSepal.Lengthの関係を見た場合、負の相関が観察されるか、回帰直線の傾きが負になるかもしれません。しかし、各Speciesごとに見た場合、傾きが正になることが示唆されています。
この場合、Speciesが交絡因子である可能性があります。なぜなら、SpeciesはSepal.WidthとSepal.Lengthの間の関係に影響を与えている可能性があります。例えば、異なる種のアイリスの場合、Sepal.WidthとSepal.Lengthの間の関係が異なるかもしれません。したがって、交絡因子としてSpeciesを考慮しないと、Sepal.WidthとSepal.Lengthの間の関係を適切に解釈することができません。
交絡因子を適切に扱うためには、統計的な手法や分析手法を用いて、交絡因子を制御する必要があります。例えば、多変量解析や回帰分析において、Speciesを説明変数としてモデルに含めることができます。そうすることで、Speciesの効果を考慮したSepal.WidthとSepal.Lengthの関係をより正確に評価できます。
したがって、交絡因子としてSpeciesを考慮することは重要です。それにより、変数間の関係をより正確に理解し、結果の解釈に偏りが生じないようにすることができます。
21.4 世界開発指標(WDI)からの例
21.4.1 出生時の平均寿命(life expectancy at birth)
- SP.DYN.LE00.IN: Life expectancy at birth, total (years)
#> Rows: 16758 Columns: 5
#> ── Column specification ────────────────────────────────────
#> Delimiter: ","
#> chr (3): country, iso2c, iso3c
#> dbl (2): year, lifeExp
#>
#> ℹ Use `spec()` to retrieve the full column specification for this data.
#> ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.
wdi_lifeExp |> filter(country == "World") |> drop_na(lifeExp) |>
ggplot(aes(year, lifeExp)) + geom_point() +
geom_smooth(method = "lm", se = FALSE)
#> `geom_smooth()` using formula = 'y ~ x'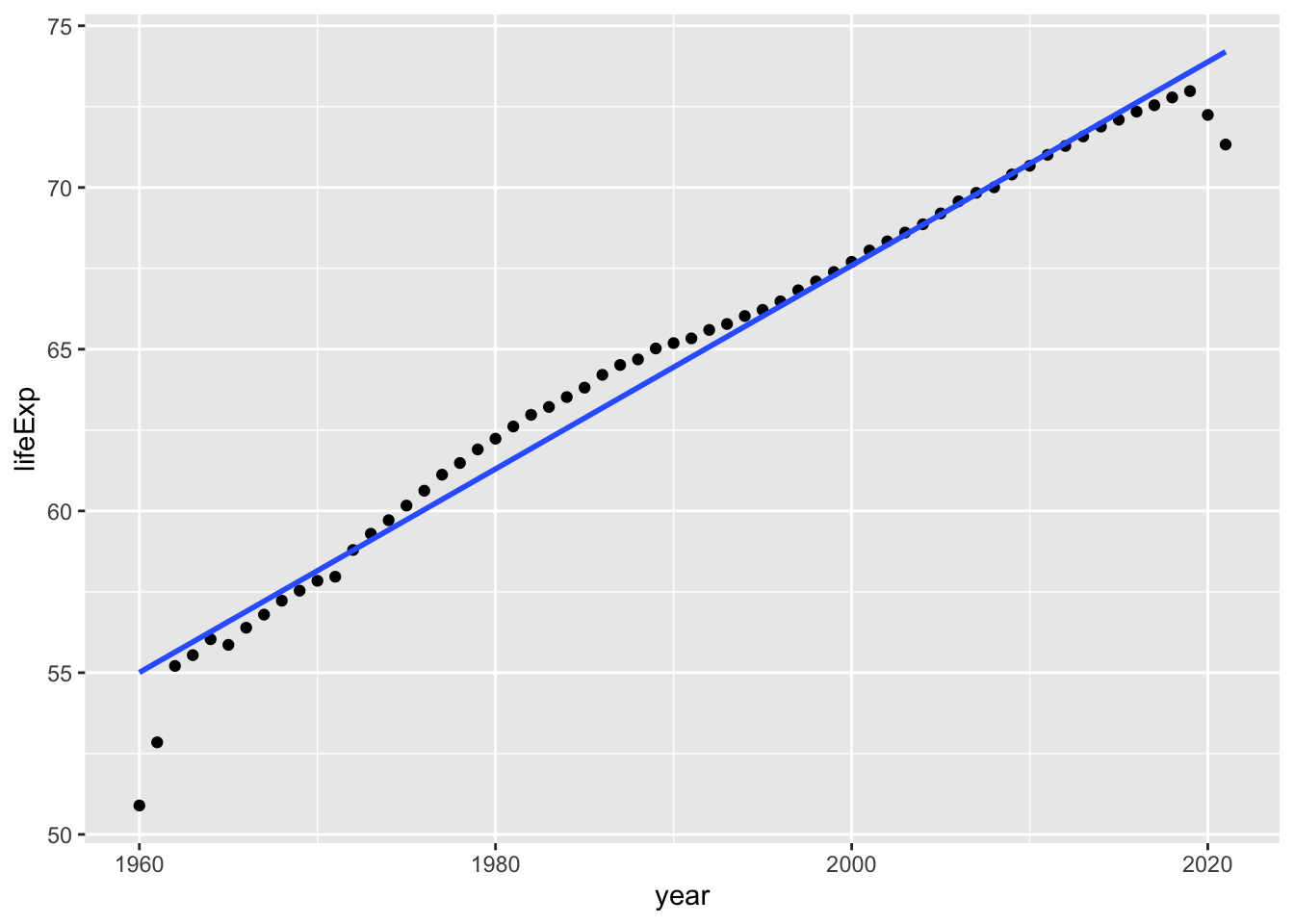
wdi_lifeExp |> lm(lifeExp ~ year, data = _) |> summary()
#>
#> Call:
#> lm(formula = lifeExp ~ year, data = wdi_lifeExp)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -51.173 -7.150 1.741 7.794 18.782
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) -5.383e+02 8.583e+00 -62.71 <2e-16 ***
#> year 3.027e-01 4.312e-03 70.20 <2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 9.707 on 15864 degrees of freedom
#> (892 observations deleted due to missingness)
#> Multiple R-squared: 0.237, Adjusted R-squared: 0.237
#> F-statistic: 4928 on 1 and 15864 DF, p-value: < 2.2e-16\[lifeExp \sim -538.3 + 0.3027 \cdot year\]
世界の平均寿命は、毎年、ほぼ、0.3年ほど増加しているという傾向にあるということのようです。ただ、適合度は、0.237 ですから、あまり良くはありません。これを使って、将来について予測するのは、適切ではないかもしれません。
Each year, life expectancy at birth increases approximately 0.3 years. R-squared of this model is 0.237, and the model explains 24%.
しかしグラフをみると、1960年ごろと、1920年以降は、ちょっと違った動きをしています。これを、除くと、ほぼ一直線上にあるように見えます。年を 1962年から、2019年までに、制限してみてみましょう。
wdi_lifeExp %>% filter(country == "World", year >= 1962, year <= 2019) %>% drop_na(lifeExp) %>% lm(lifeExp ~ year, .) %>% summary()
#>
#> Call:
#> lm(formula = lifeExp ~ year, data = .)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -1.00776 -0.29546 -0.04527 0.37540 0.82117
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) -5.537e+02 7.841e+00 -70.62 <2e-16 ***
#> year 3.107e-01 3.939e-03 78.89 <2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.5022 on 56 degrees of freedom
#> Multiple R-squared: 0.9911, Adjusted R-squared: 0.9909
#> F-statistic: 6224 on 1 and 56 DF, p-value: < 2.2e-16今度は、決定係数が 0.9911 になりました。グラフをみた直感とあっていますね。ですから、1962年から、2019年までの間は、世界の出生時平均寿命は、毎年、0.31 年ほどずつ増加していると結論することができそうです。
実際には、調査対象の国がどのように変化しているかなど、他の要因も調べる必要があると思います。
また、なぜ、1960年から、1962年は、大きく変化しているのか、2020年で減少している理由はなんだろうか。コロナウイルス感染症のせいだろうかなど、考えることが広がっていくかもしれません。次々と新しい問いが出てくること。それが素晴らしいことです。ほんの少しわかったことによって、扉が開いていく。そのような経験をたくさんしていただきたいと思います。
21.4.2 BRICS の出生時
今度は、BRICS についてみてみましょう。最初は、BRIC または、BRICs と、4カ国で、ブラジル、ロシア、インド、中国を指していましたが、南アフリカが急成長したこともあり、南アフリカを加えて、現在は、BRICS と言っているようです。2023 年の首脳会議で、さらに、6カ国(アルゼンチン、エジプト、エチオピア、イラン、サウジアラビア、アラブ首長国連邦)が加わって、かなり大きな勢力となりつつあるようです。どのぐらいの規模なのか、GDP(国内総生産)、Population(人口)、Oil Production(原油生成量)、Exports of Goods (製品輸出)などが世界のどの程度をしめるのかも、そして、これらの指標の増加・または減少の傾向などについても、調べてみると良いかもしれませんね。
決定係数を求めてみましょう。下から、0.47 ですから、まあまあです。
mod_brics <- wdi_lifeExp |>
filter(country %in% c("Brazil", "Russian Federation", "India", "China", "South Africa")) |>
drop_na(lifeExp) |>
lm(lifeExp ~ year, data = _) %>% summary()
mod_brics$r.squared
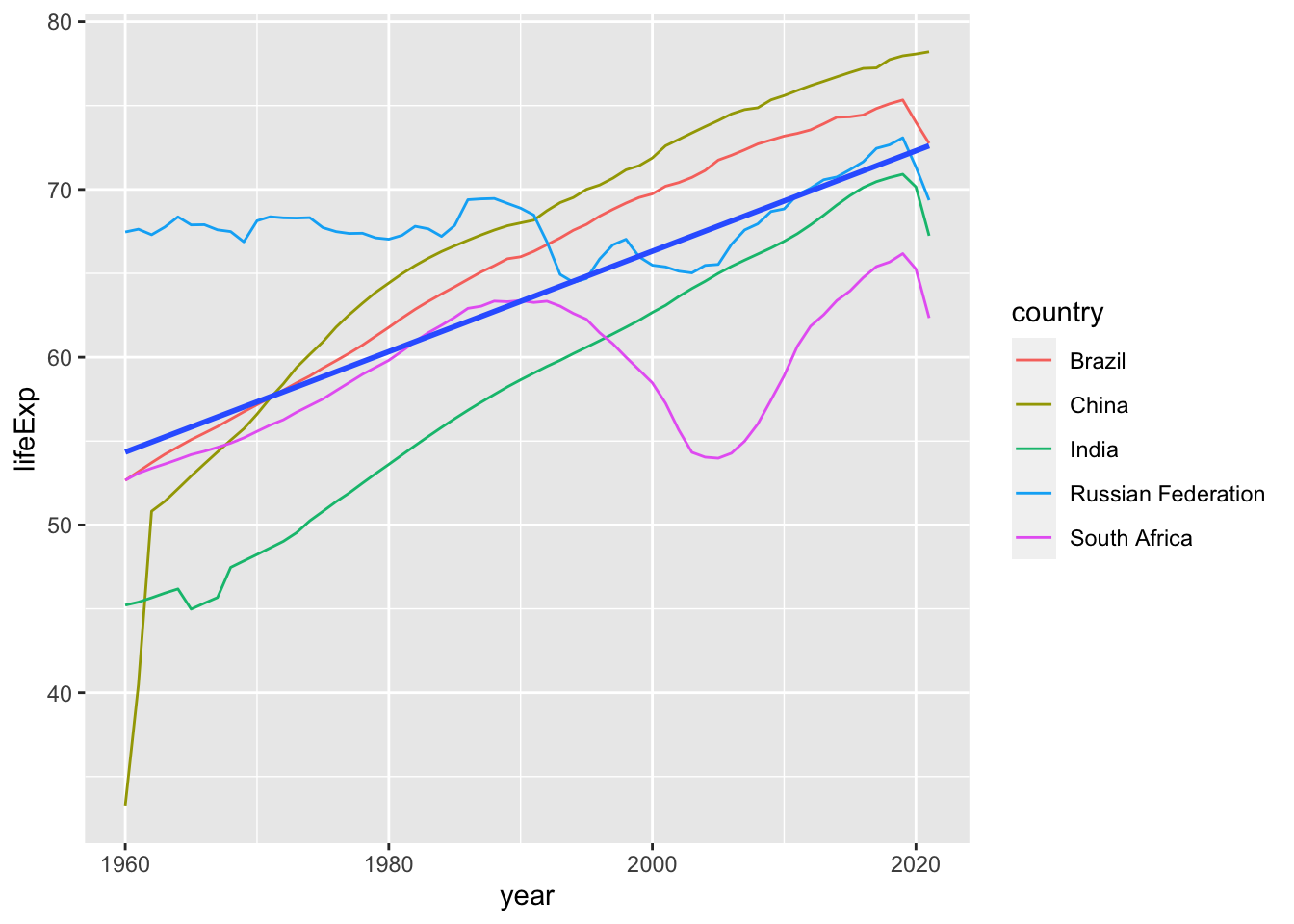
#> [1] 0.4717945そこで、4カ国の、出生時平均寿命のグラフを描いてみましょう。回帰直線は、データポイント(点)から計算されるものですから、geom_point() を使った方が良いかもしれませんが、ある程度長い期間の時系列データですから、geom_line() で、折れ線グラフを書いてみました。geom_line() の中にある、color = country を省略するとどうなるでしょうか。ぜひ試してみてください。geom_point() にかえたグラフも描いてみることをお勧めします。
wdi_lifeExp |>
filter(country %in% c("Brazil", "Russian Federation", "India", "China", "South Africa")) |>
drop_na(lifeExp) |>
ggplot(aes(year, lifeExp)) + geom_line(aes(color = country)) +
geom_smooth(formula = y~x, method = "lm", se = FALSE)国ごとにかなり異なることもわかりますね。それも、かなりの変化があります。この場合には、いろいろなモデルのさまざまな値をみるよりも、グラフをていねいにみていくことが大切なように思います。
一応、geom_point() に変更し、それぞれの国ごとに、回帰直線を描いたグラフを付けておきます。
wdi_lifeExp |>
filter(country %in% c("Brazil", "Russian Federation", "India", "China","South Africa")) |>
drop_na(lifeExp) |>
ggplot(aes(year, lifeExp, color = country)) + geom_point() +
geom_smooth(formula = y~x, method = "lm", se = FALSE) + facet_wrap(~country)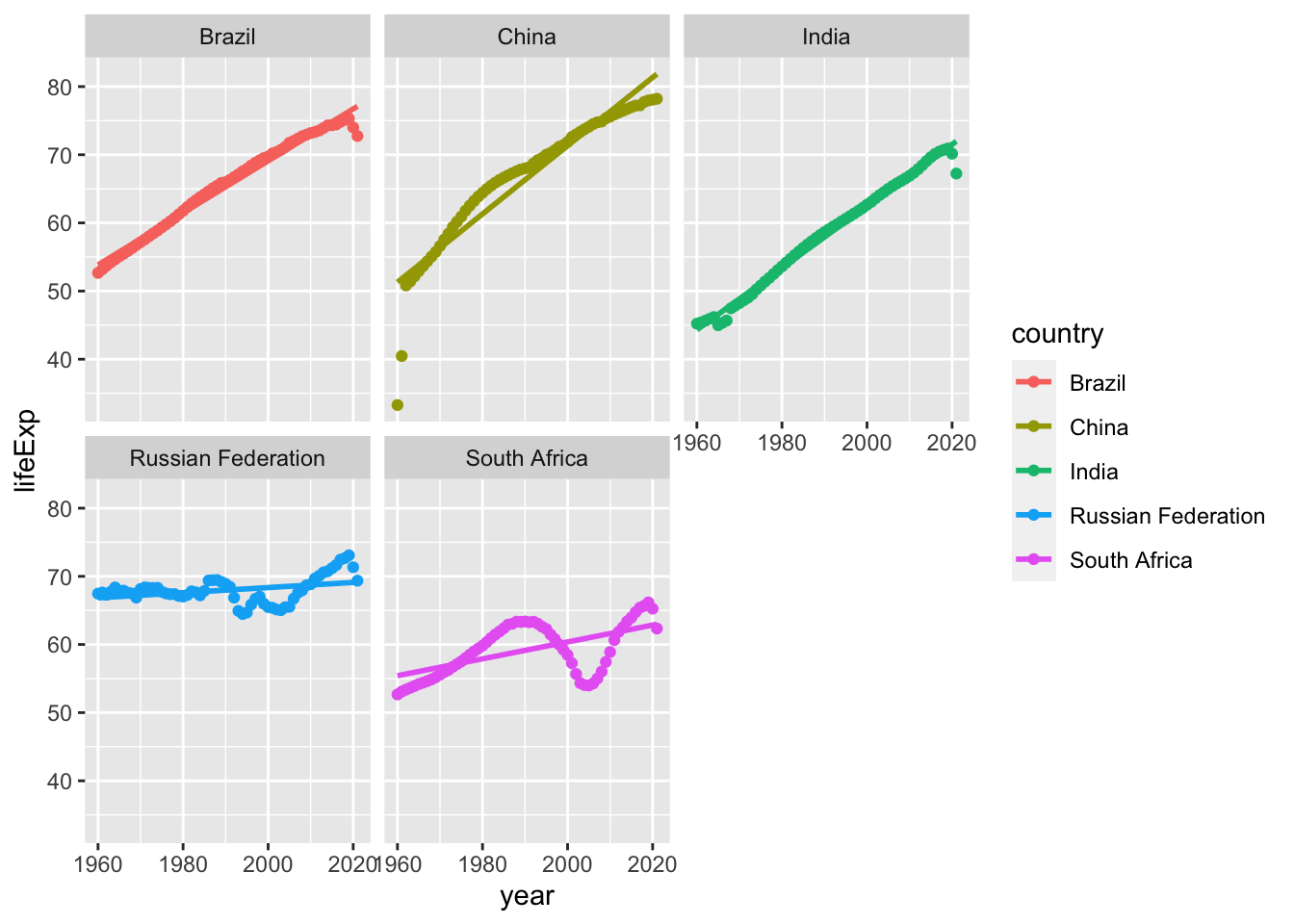
以下では、それぞれの国ごとに、モデルを作成し tidy や、glance で、その、基本的なデータを、取り出して、表にする方法を紹介します。このようにして、一度に、国ごとのモデルの、さまざまな値を求めることができます。結果だけを出力することも可能ですが、ステップごとの状況も確認できるようにしておきます。
country_model <- function(df) {
lm(lifeExp ~ year, data = df)
}
by_country <- wdi_lifeExp |>
filter(country %in% c("Brazil", "Russian Federation", "India", "China","South Africa")) |>
drop_na(lifeExp) |> group_by(country) |> nest()
by_country