32 探索的データ解析

32.1 探索的データ解析 (EDA)とは

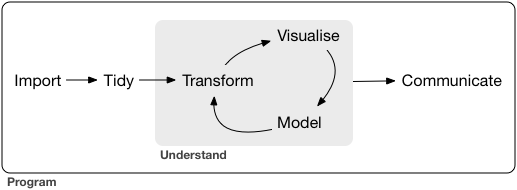
image from r4ds

探索的データ解析 (EDA) は、データを理解するための反復的なサイクルです。EDAでは、以下のことを行います。

データに関する問いを作成する
データの可視化、変形・整形、モデリングによって、問いの答えを探索する。
学んだことを使って、問いをより洗練されたものとする。

EDAは、あらゆるデータ分析において重要な役割を担います。EDA によって、課題解決のいとぐちを発見することもありますし、他の課題との関係性を発見する場合もあります。EDAを使用してデータの問題や品質を確認したり、データが信頼できるものであるかを見極める問いを作成できる場合もあります。

32.2 探索的データ解析 (EDA) の一例

WDI の一つの指標を使って、流れを見てみましょう。

32.2.1 データの取得と読み込み - Data Import

NY.GDP.PCAP.CD: GDP per capita (current US$)

df_wdi_gdppcap <- WDI(country = "all", indicator = c(gdp_pcap = "NY.GDP.PCAP.CD"))
write_csv(df_wdi_gdppcap, "./data/df_wdi_gdppcap.csv")

df_wdi_gdppcap

32.2.2 データ変形・整形 - Data Transformation

32.2.2.1 列を `select`

どの変数について分析するかを選ぶ。

df_wdi_gdppcap_small <- df_wdi_gdppcap %>% 
  select(country, year, gdp_pcap)
df_wdi_gdppcap_small

32.2.2.2 行を `filter`

いくつかの国に、フォーカスして調べる。

df_wdi_gdppcap_short <- df_wdi_gdppcap %>% 
  filter(country %in% c("Japan", "Germany", "United States"))
df_wdi_gdppcap_short

列（変数）と、行（国）の選択を続けて、実行すると次のようになる。一つ一つ変形したデータ（オブジェクト）に名前をつけて、保存する必要がないので、パイプ（%>%）の活用は有用である。

df_wdi_gdppcap_small_short <- df_wdi_gdppcap %>% select(country, year, gdp_pcap) %>%
  filter(country %in% c("Japan", "Germany", "United States"))
df_wdi_gdppcap_small_short

32.2.3 可視化 Data Visualization

次は、よく生じる、誤りの例で、ノコギリの歯（sawtoothed）のようなギザギザ・グラフと呼ばれます。なぜこのようなことが起きているかわかりますか。

df_wdi_gdppcap_small_short %>%
  ggplot(aes(x = year, y = gdp_pcap)) + geom_line()
#> Warning: Removed 1 row containing missing values
#> (`geom_line()`).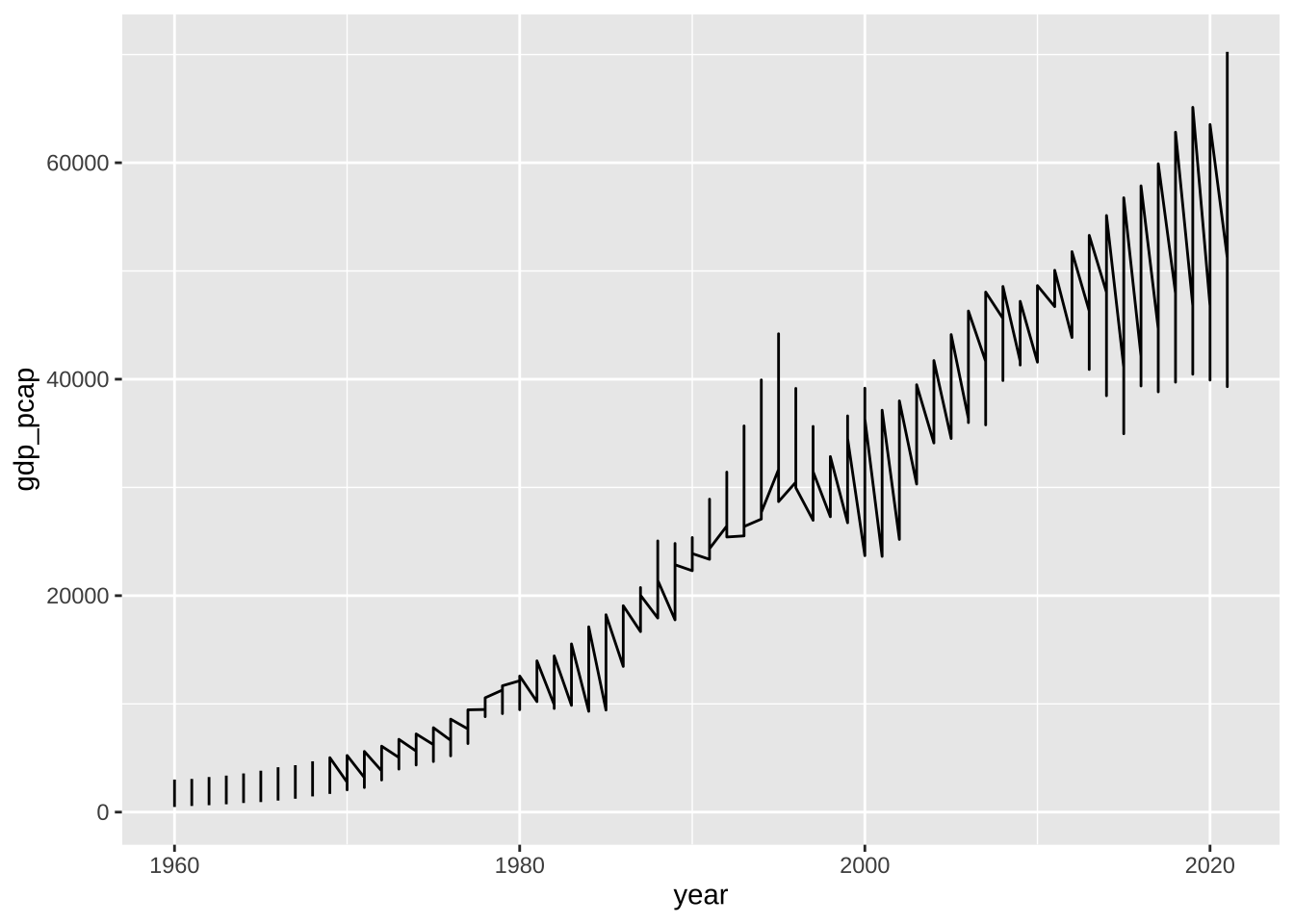

同じ年に、多くのデータがあるので、折れ線グラフを適切に書くことができませんでした。

df_wdi_gdppcap_small_short %>% filter(country %in% c("Japan")) %>%
  ggplot(aes(x = year, y = gdp_pcap)) + geom_line()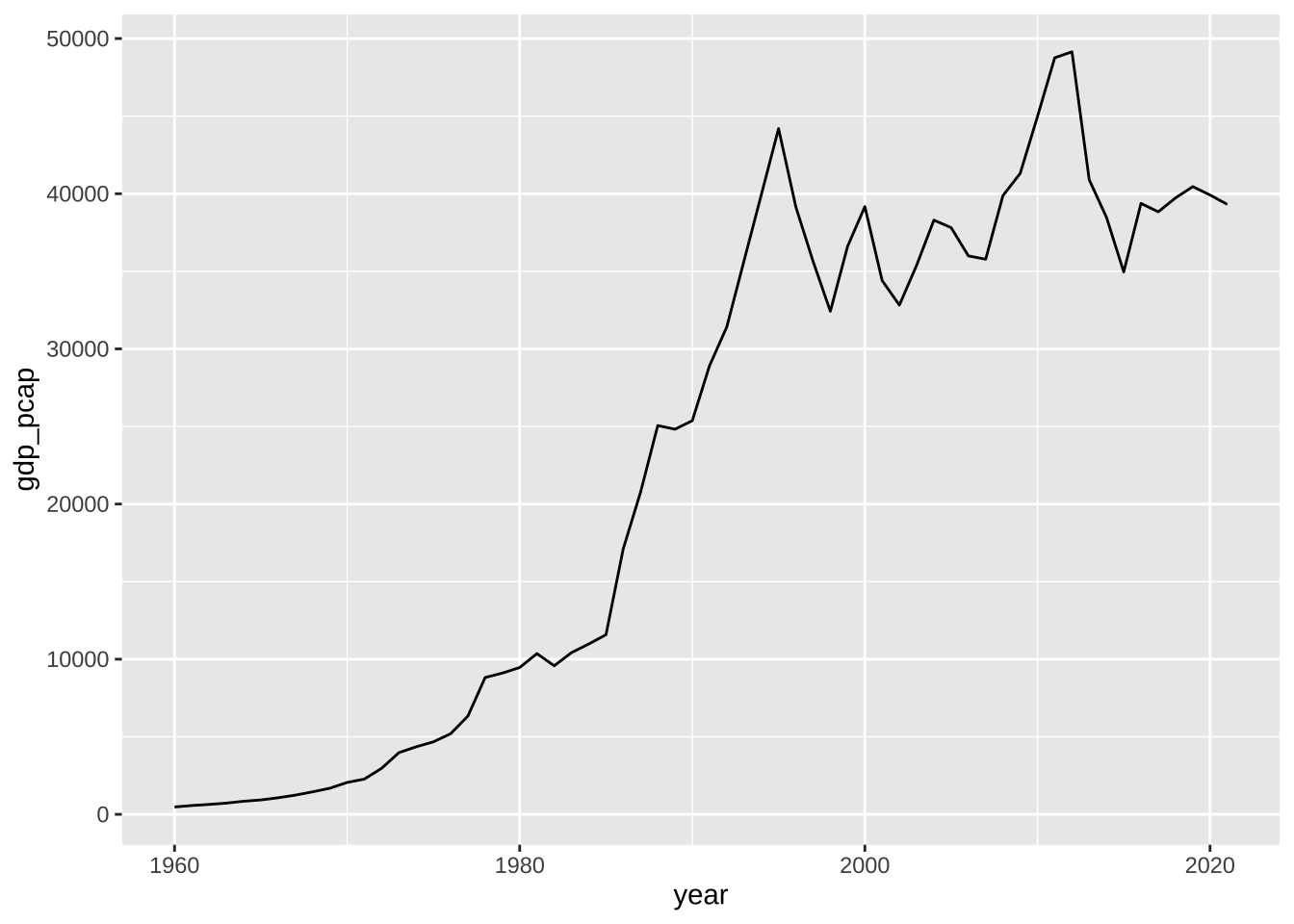

一般的には、散布図をまず、書いてみるのも一つです。

df_wdi_gdppcap_small_short %>%
  ggplot(aes(x = year, y = gdp_pcap)) + geom_point()
#> Warning: Removed 10 rows containing missing values
#> (`geom_point()`).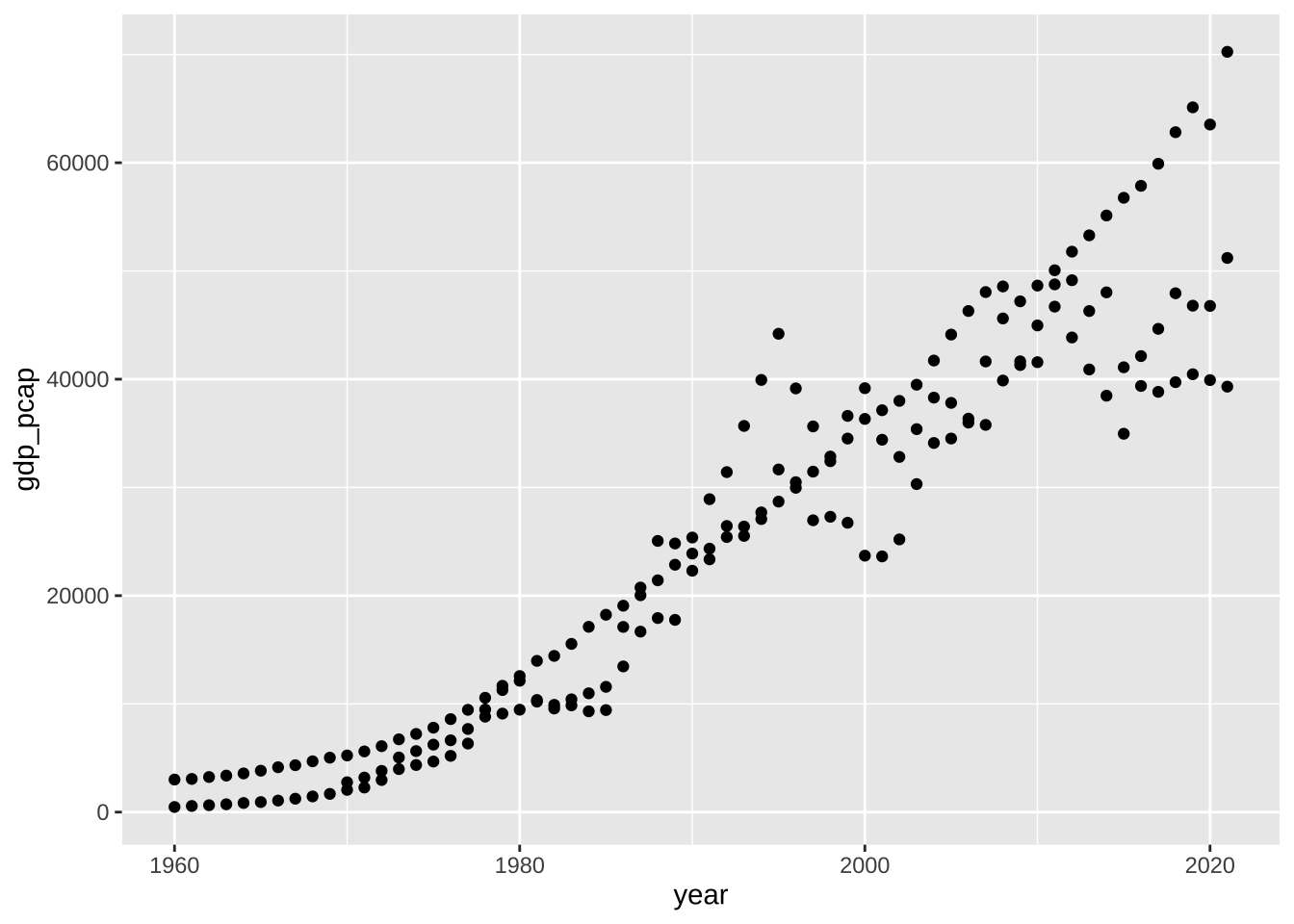

国別に、異なる色を使うことで、折れ線グラフを書くことも可能です。

df_wdi_gdppcap_small_short %>% drop_na(gdp_pcap) %>%
  ggplot(aes(x = year, y = gdp_pcap, col = country)) + geom_line()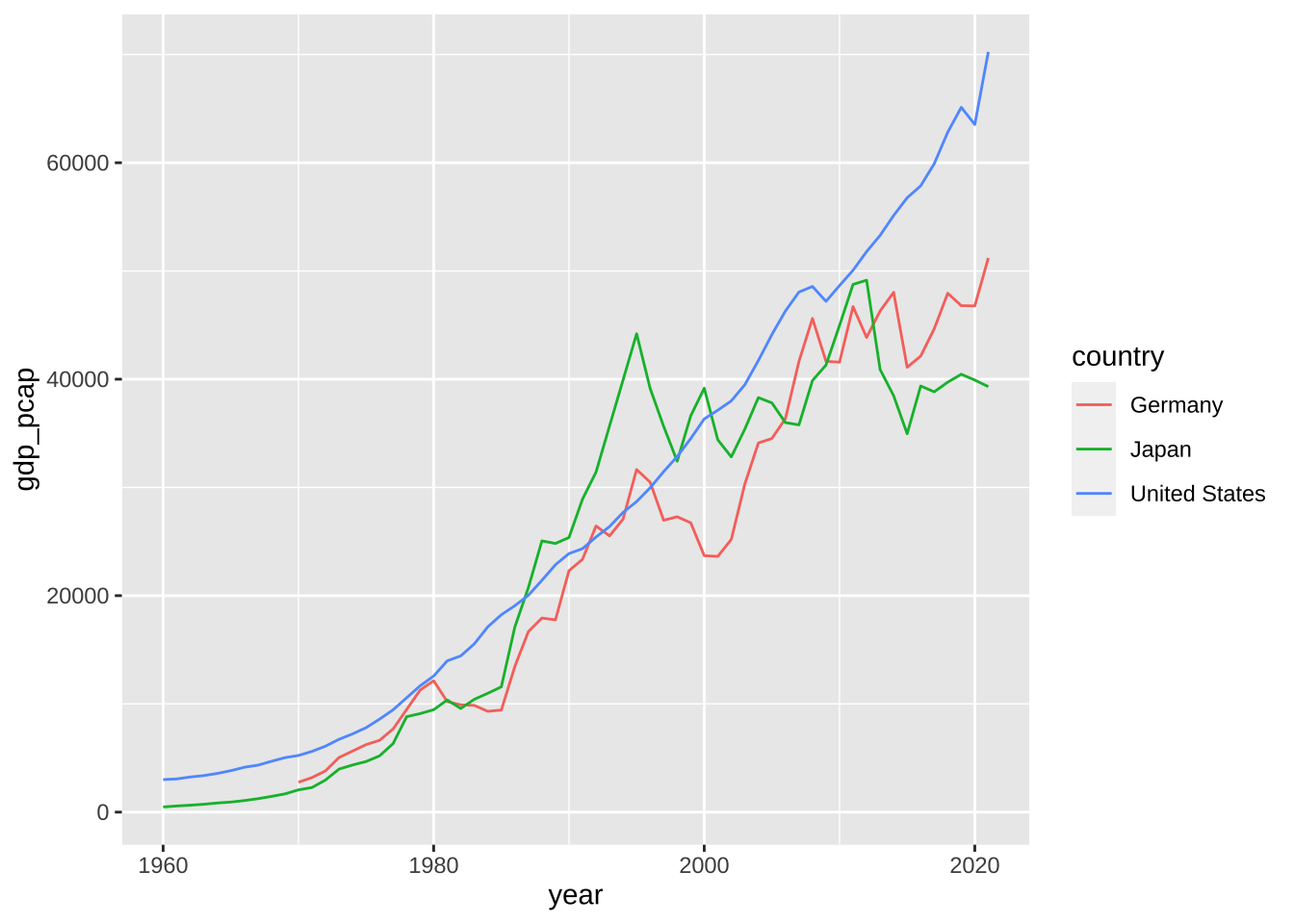

折線グラフと、散布図を同時に描くこともかのうです。

df_wdi_gdppcap_small_short %>% drop_na(gdp_pcap) %>%
  ggplot(aes(x = year, y = gdp_pcap, col = country)) + geom_line() +
  geom_point()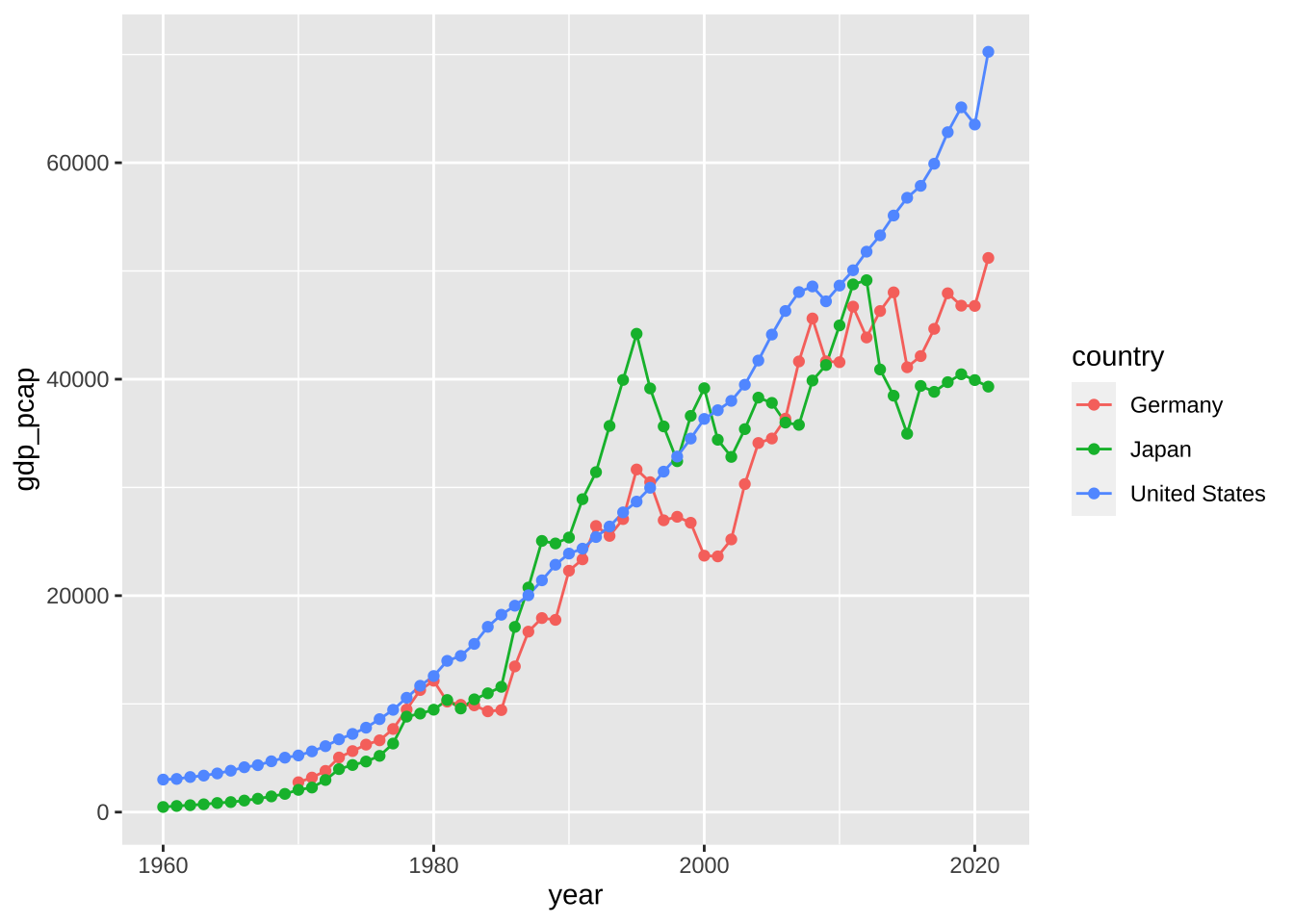

点を、曲線で近似する方法はいくつも知られているが、ある幅で、近似していく、LOESS が初期値となっている。method='loess' を省略しても、同じ近似がなされる。span という値を調節することで、ことなる幅での近似曲線を書くことも可能である。初期値は、0.75。

df_wdi_gdppcap_small_short %>% drop_na(gdp_pcap) %>%
  ggplot(aes(x = year, y = gdp_pcap)) + 
  geom_point(aes(color = country)) + 
  geom_smooth(method = 'loess', formula = 'y ~ x')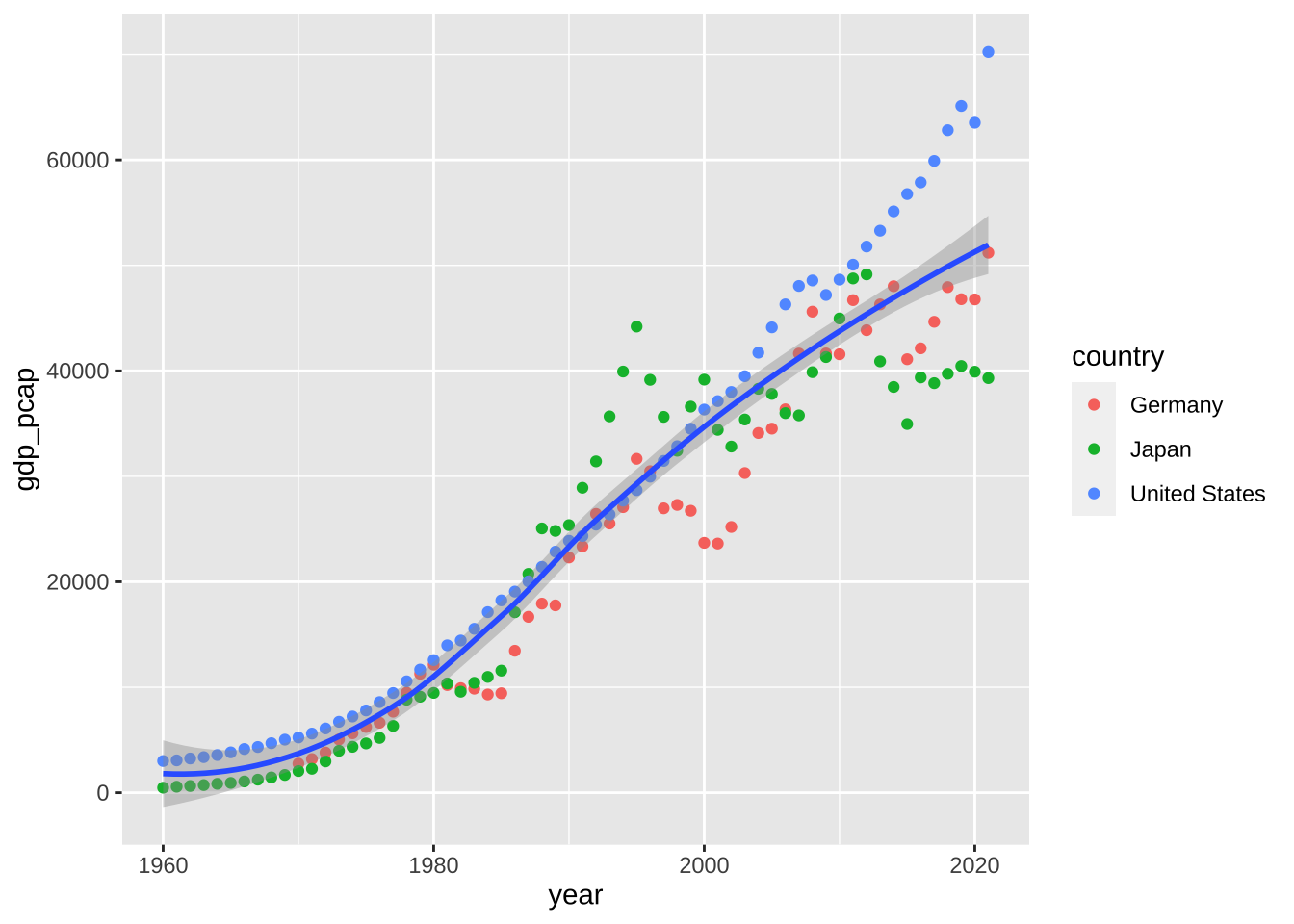

32.2.4 データモデリング Data Modeling

上の例では、曲線ではなく、直線で近似することも考えられる。

df_wdi_gdppcap_small_short %>% drop_na(gdp_pcap) %>%
  ggplot(aes(x = year, y = gdp_pcap)) + 
  geom_point(aes(color = country)) + 
  geom_smooth(method = 'lm', formula = 'y ~ x')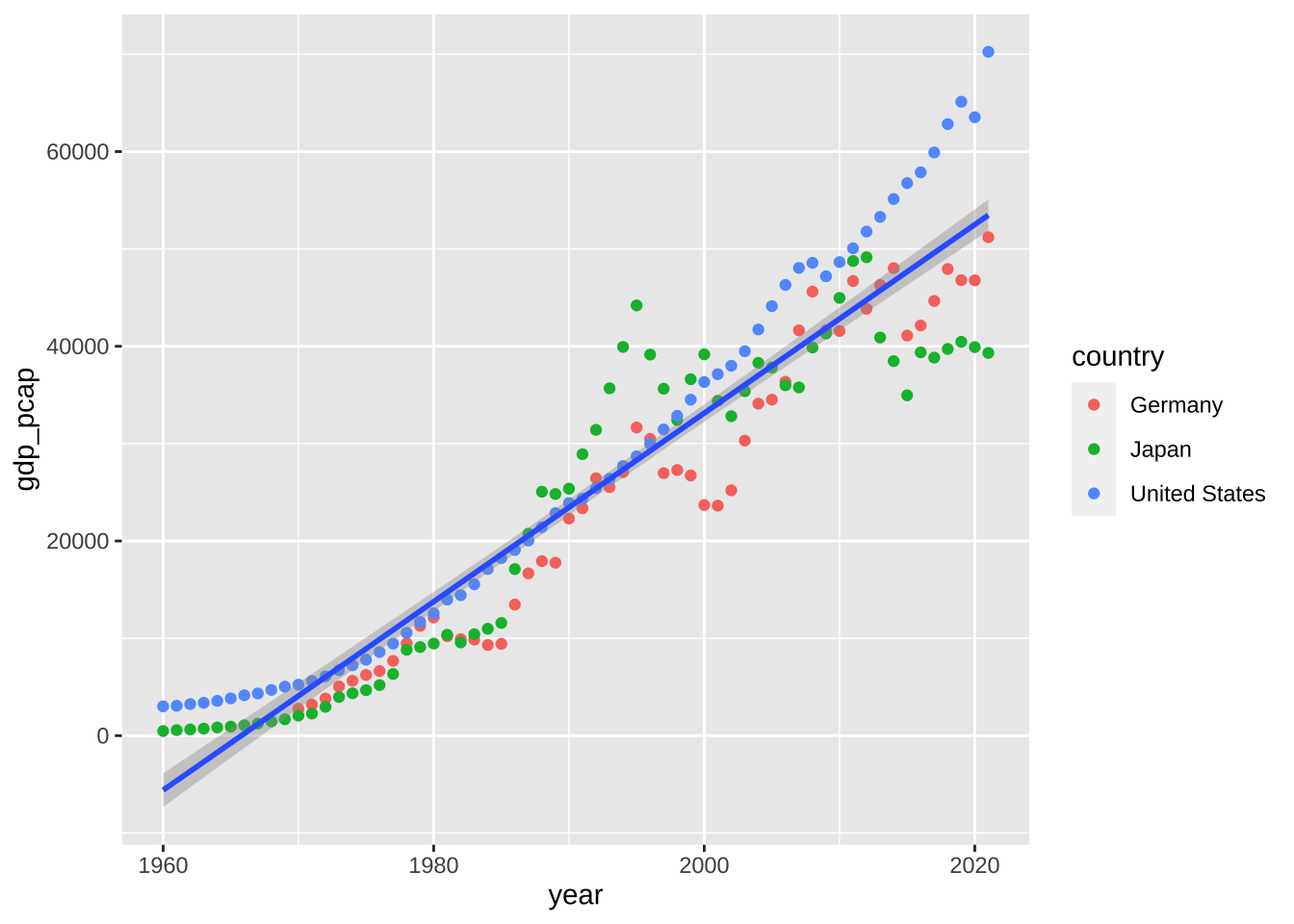

簡単な線形回帰モデルでの、回帰直線の y-切片や、傾きは、次のコードで与えられ、p-value や、R squared の値も求められる。

この例では、年とともに、増加の傾向があること。そして、線形モデルが$$、90% 程度説明していると表現される。すなわち、

は、良い、近似であることがわかる。

df_wdi_gdppcap_small_short %>% lm(gdp_pcap ~ year, .) %>% summary()
#> 
#> Call:
#> lm(formula = gdp_pcap ~ year, data = .)
#> 
#> Residuals:
#>      Min       1Q   Median       3Q      Max 
#> -14156.8  -3200.5   -507.4   3237.7  16779.2 
#> 
#> Coefficients:
#>               Estimate Std. Error t value Pr(>|t|)    
#> (Intercept) -1903497.5    48007.9  -39.65   <2e-16 ***
#> year             968.3       24.1   40.18   <2e-16 ***
#> ---
#> Signif. codes:  
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 5514 on 174 degrees of freedom
#>   (10 observations deleted due to missingness)
#> Multiple R-squared:  0.9027, Adjusted R-squared:  0.9021 
#> F-statistic:  1614 on 1 and 174 DF,  p-value: < 2.2e-16

31 その他のデータベース

33 視覚化の詳細