Chapter 8 Topics in Exploratory Data Analysis II　

Lecture by Prof. Keisuke Ishibashi and R Notebook Compiled by HS

Project

Classification
Example: simple guessing by sepal length
Example: classification by sepal length using glm
Evaluation of classifications
Example: classification with various combinations
Evaluation
Summary of Classification
References

8.1 Classification IRIS dataset

8.1.1 Setup

library(tidyverse)
library(modelr) # a part of tidyverse package but not a core and need to load
library(modelsummary) # handy comparison introduced by Prof. Kaizoji
library(datasets) # attached as default

8.1.2 Data: `iris`

We want to consider a problem to classify iris by species using the data provided.

data(iris) # renew the data
head(iris)

##   Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 1          5.1         3.5          1.4         0.2  setosa
## 2          4.9         3.0          1.4         0.2  setosa
## 3          4.7         3.2          1.3         0.2  setosa
## 4          4.6         3.1          1.5         0.2  setosa
## 5          5.0         3.6          1.4         0.2  setosa
## 6          5.4         3.9          1.7         0.4  setosa

Since it is easier to handle data and we add many columns later, we shorten the column names.

iris_tbl <- as_tibble(iris) #%>%
colnames(iris_tbl) <- c("sl", "sw", "pl", "pw", "species")
#rename(sl = Sepal.Length, sw = Sepal.Width, pl = Petal.Length, pw = Petal.Width, species = Species)
iris_tbl

## # A tibble: 150 × 5
##       sl    sw    pl    pw species
##    <dbl> <dbl> <dbl> <dbl> <fct>  
##  1   5.1   3.5   1.4   0.2 setosa 
##  2   4.9   3     1.4   0.2 setosa 
##  3   4.7   3.2   1.3   0.2 setosa 
##  4   4.6   3.1   1.5   0.2 setosa 
##  5   5     3.6   1.4   0.2 setosa 
##  6   5.4   3.9   1.7   0.4 setosa 
##  7   4.6   3.4   1.4   0.3 setosa 
##  8   5     3.4   1.5   0.2 setosa 
##  9   4.4   2.9   1.4   0.2 setosa 
## 10   4.9   3.1   1.5   0.1 setosa 
## # … with 140 more rows

Before we start, let us look at the basic imformation of the data. There are three kinds of species.

iris_tbl %>% summary()

##        sl              sw              pl              pw       
##  Min.   :4.300   Min.   :2.000   Min.   :1.000   Min.   :0.100  
##  1st Qu.:5.100   1st Qu.:2.800   1st Qu.:1.600   1st Qu.:0.300  
##  Median :5.800   Median :3.000   Median :4.350   Median :1.300  
##  Mean   :5.843   Mean   :3.057   Mean   :3.758   Mean   :1.199  
##  3rd Qu.:6.400   3rd Qu.:3.300   3rd Qu.:5.100   3rd Qu.:1.800  
##  Max.   :7.900   Max.   :4.400   Max.   :6.900   Max.   :2.500  
##        species  
##  setosa    :50  
##  versicolor:50  
##  virginica :50  
##                 
##                 
##

8.1.2.1 Visualization

The following already tell something about species.

iris_tbl %>% ggplot(aes(pw,pl, color = species)) + geom_point()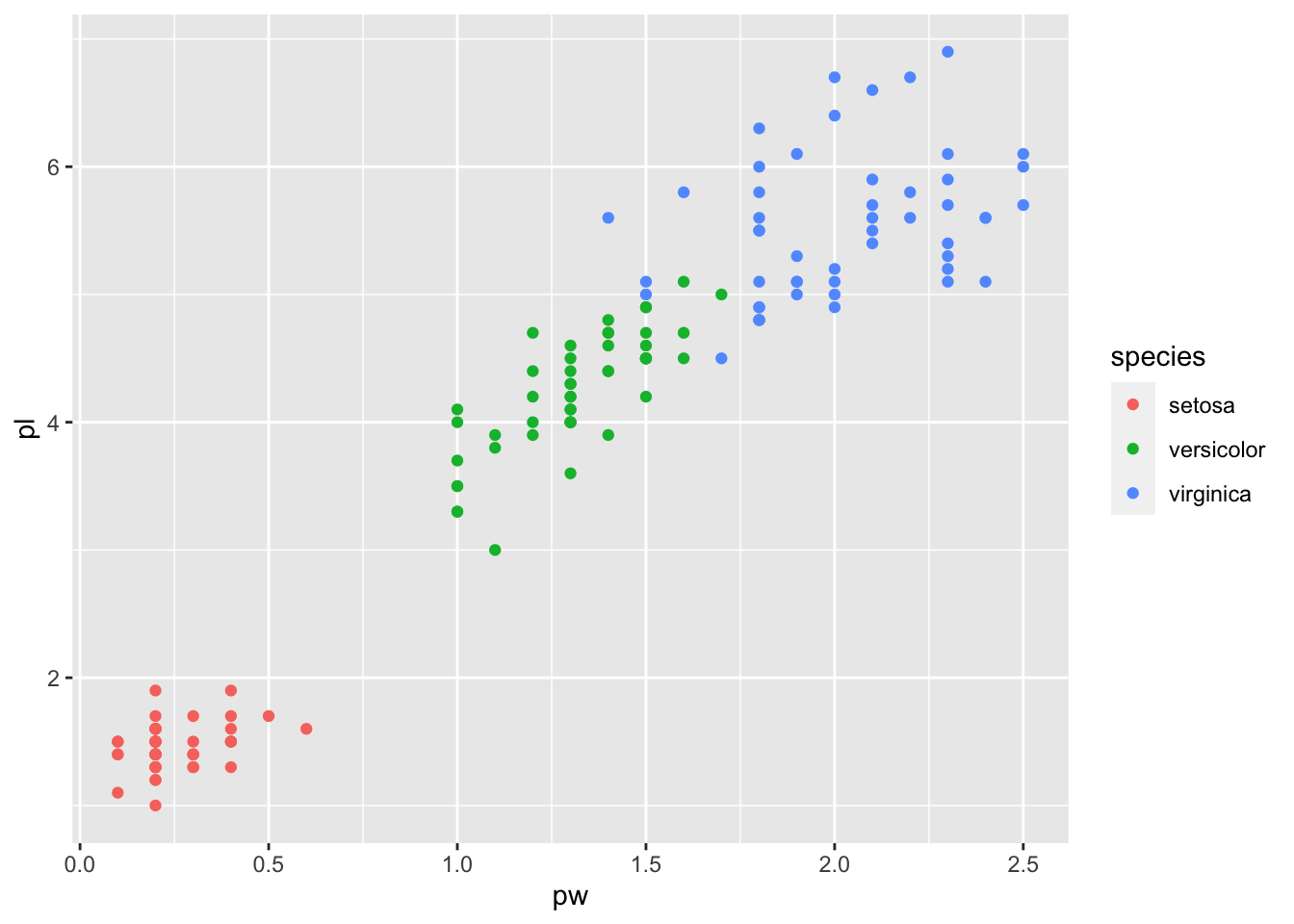

iris_tbl %>% group_by(species) %>% 
  summarize(sl_mean = mean(sl), sw_mean = mean(sw), pl_mean = mean(pl), pw_mean = mean(pw))

## # A tibble: 3 × 5
##   species    sl_mean sw_mean pl_mean pw_mean
##   <fct>        <dbl>   <dbl>   <dbl>   <dbl>
## 1 setosa        5.01    3.43    1.46   0.246
## 2 versicolor    5.94    2.77    4.26   1.33 
## 3 virginica     6.59    2.97    5.55   2.03

The mean of setosa’s petal length is very small compared with others. So it may be possible to classify setosa by petal lenght.

The following are a boxplot and a frequency polygon of the data by petal length.

iris_tbl %>% ggplot(aes(pl, fill = species)) + geom_boxplot()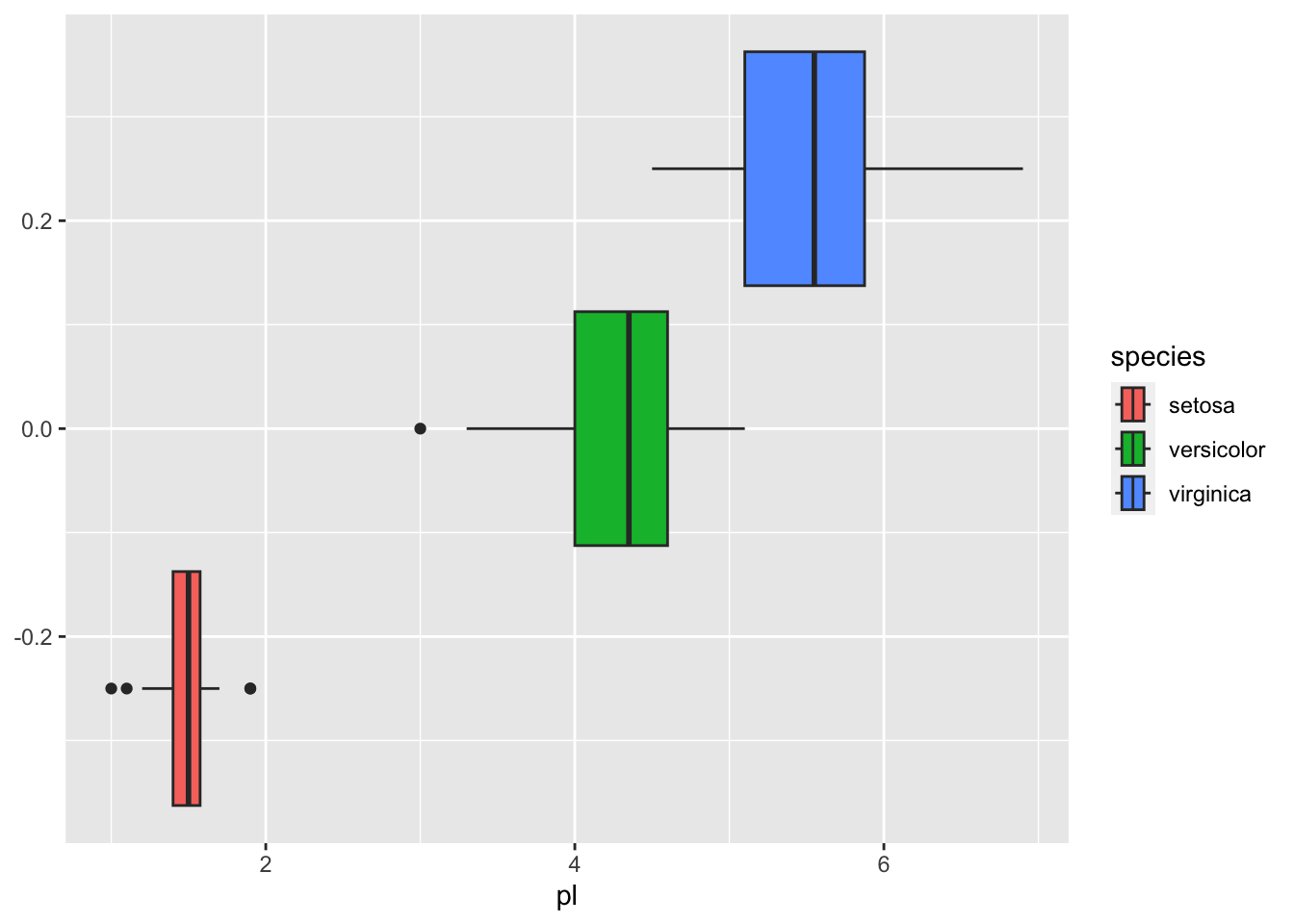

iris_tbl %>% ggplot(aes(pl, color = species)) + geom_freqpoly()

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.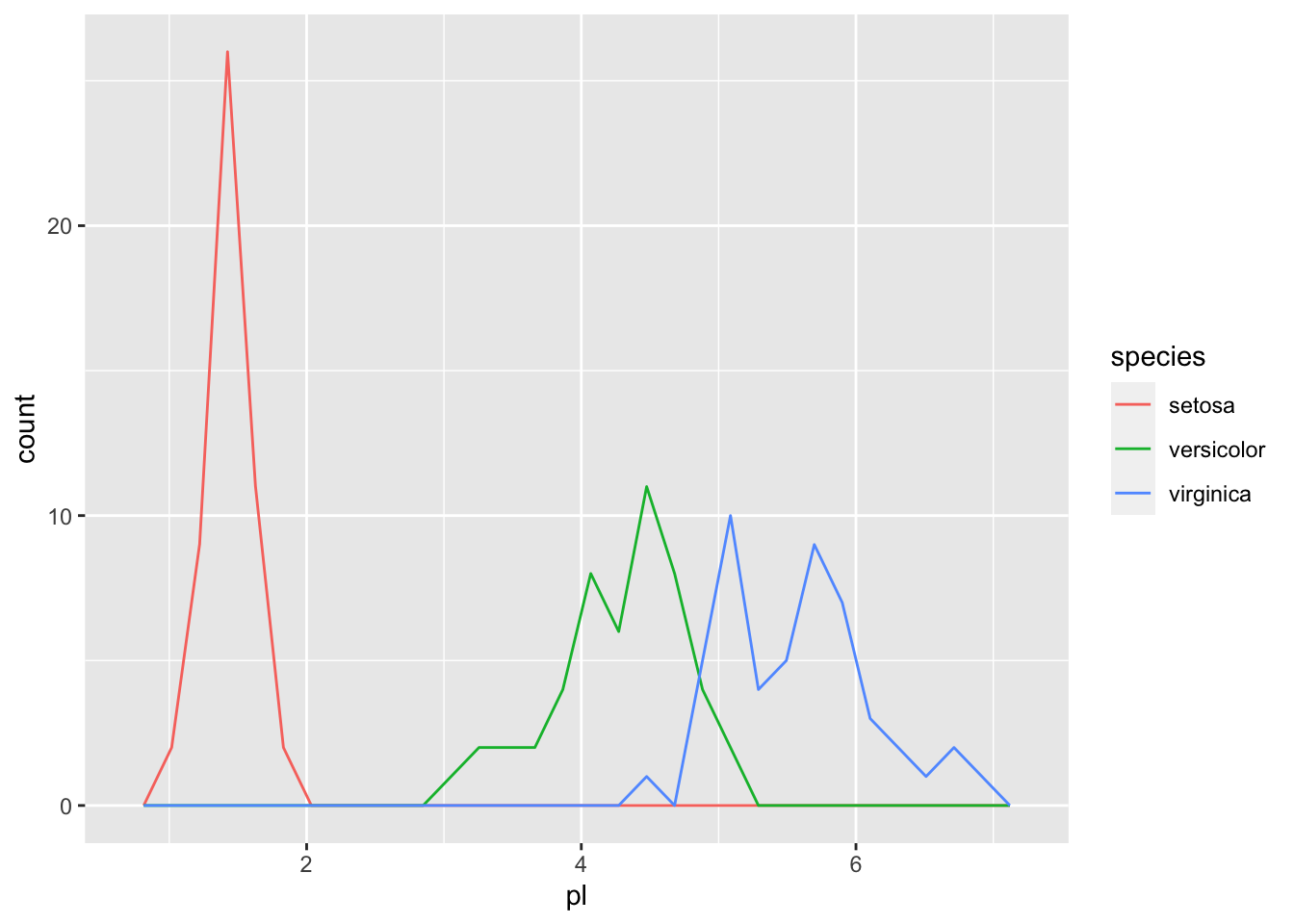

iris_tbl %>% group_by(species) %>% 
  summarize(min_of_petal_lenght = min(pl), max_of_petal_lenght = max(pl))

## # A tibble: 3 × 3
##   species    min_of_petal_lenght max_of_petal_lenght
##   <fct>                    <dbl>               <dbl>
## 1 setosa                     1                   1.9
## 2 versicolor                 3                   5.1
## 3 virginica                  4.5                 6.9

Hence if we set the threshhold to be around 2.5, we can separate setosa.

iris_tbl2 <- iris_tbl %>% filter(pl >= 2.5)
summary(iris_tbl2)

##        sl              sw              pl              pw       
##  Min.   :4.900   Min.   :2.000   Min.   :3.000   Min.   :1.000  
##  1st Qu.:5.800   1st Qu.:2.700   1st Qu.:4.375   1st Qu.:1.300  
##  Median :6.300   Median :2.900   Median :4.900   Median :1.600  
##  Mean   :6.262   Mean   :2.872   Mean   :4.906   Mean   :1.676  
##  3rd Qu.:6.700   3rd Qu.:3.025   3rd Qu.:5.525   3rd Qu.:2.000  
##  Max.   :7.900   Max.   :3.800   Max.   :6.900   Max.   :2.500  
##        species  
##  setosa    : 0  
##  versicolor:50  
##  virginica :50  
##                 
##                 
##

Since it looks difficult to classify versicolor and virginica only by petal length, let us look at other variables.

iris_tbl %>% ggplot(aes(sl,pl, color = species)) + geom_point()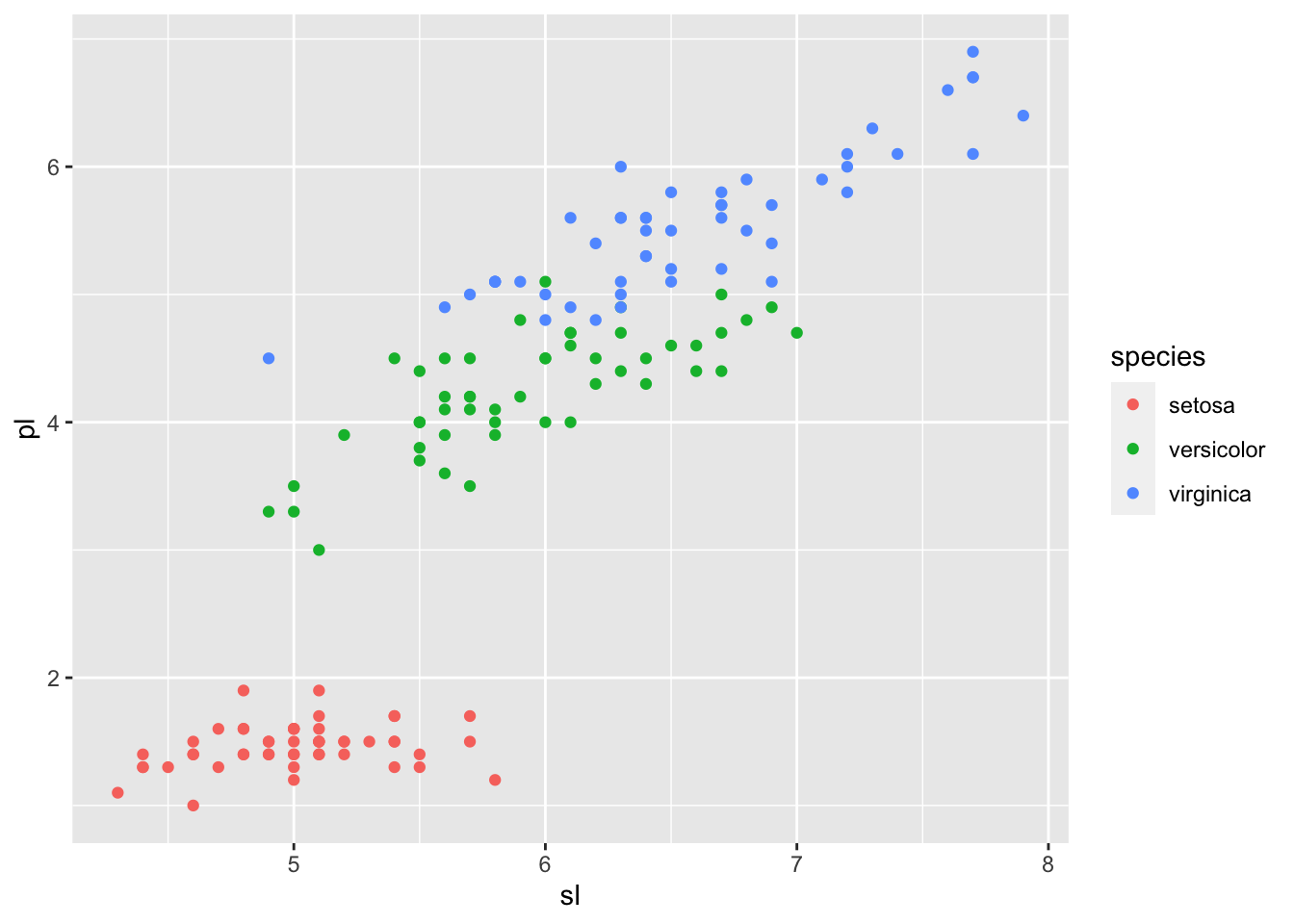

8.1.2.2 Sepal Length

You can find different features of charts, boxplots and frequency polygons of sepal length.

iris_tbl2 %>% ggplot(aes(sl, fill = species)) + geom_boxplot()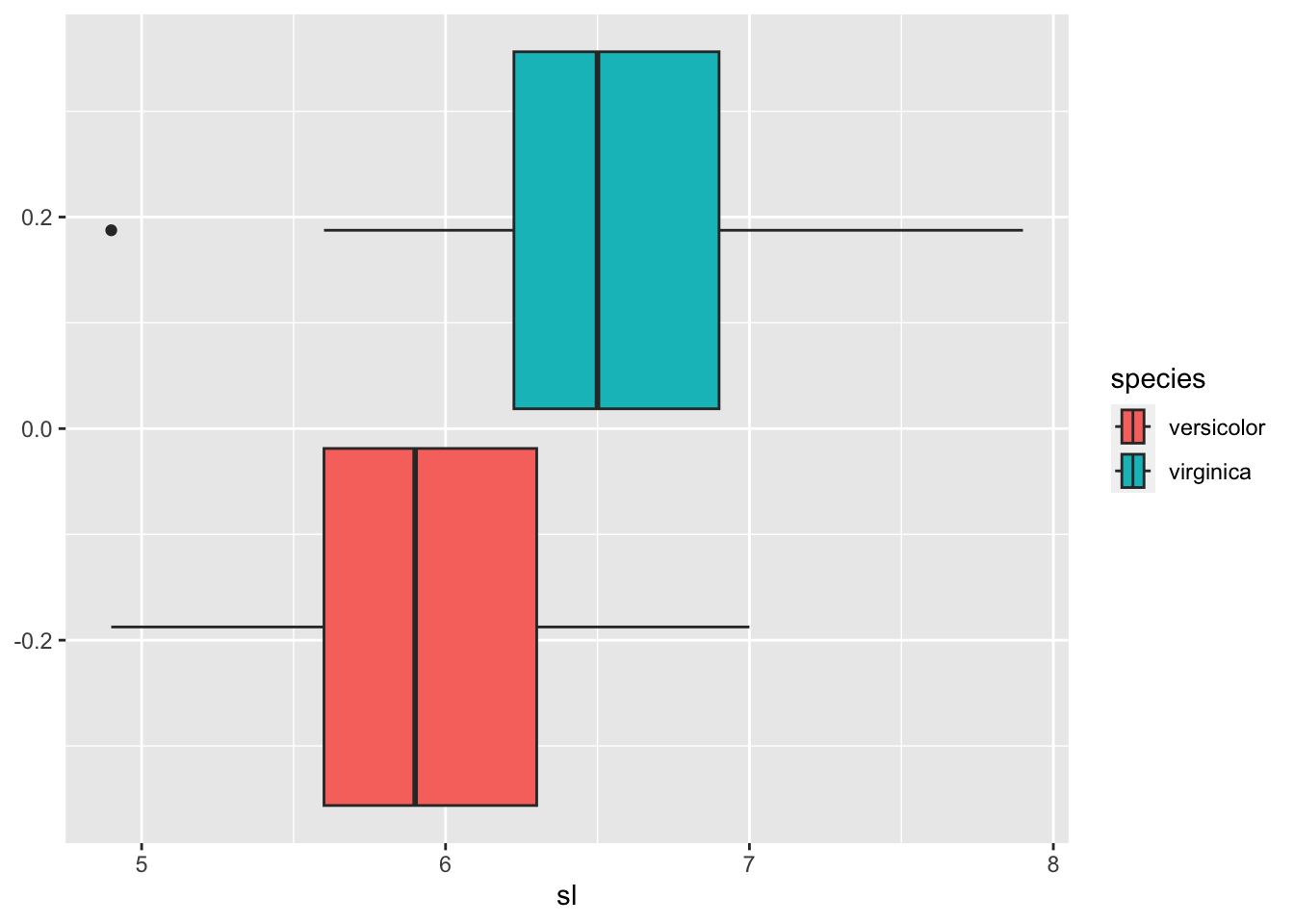

iris_tbl2 %>% ggplot(aes(sl, color = species)) + geom_freqpoly()

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.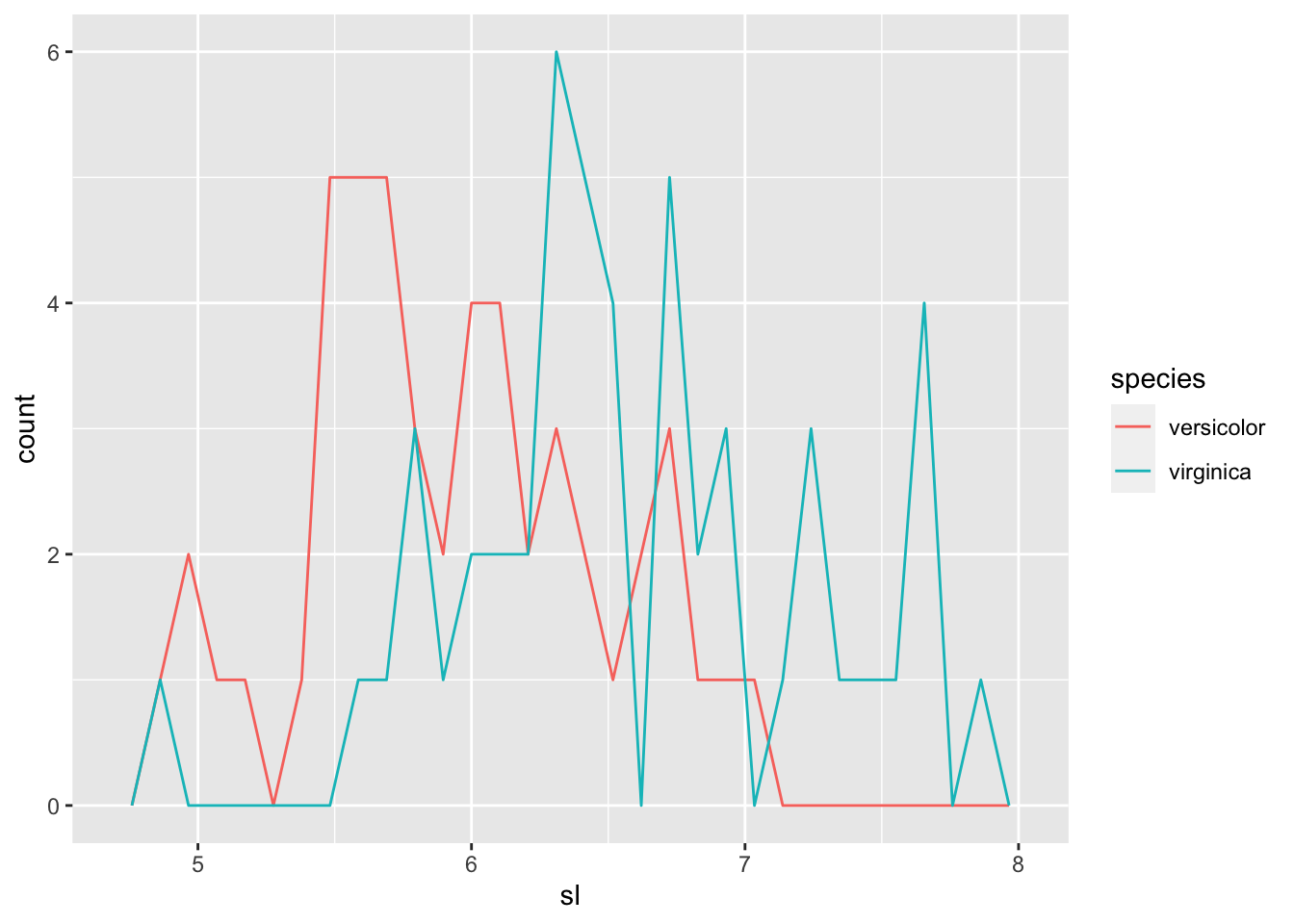

8.1.3 Binary classification

Let us set a numerical marker 1 to virginica.

iris_tbl2ext <- iris_tbl2 %>% 
  mutate(virginica = as.numeric(species == 'virginica'))
iris_tbl2ext %>% arrange(-virginica)

## # A tibble: 100 × 6
##       sl    sw    pl    pw species   virginica
##    <dbl> <dbl> <dbl> <dbl> <fct>         <dbl>
##  1   6.3   3.3   6     2.5 virginica         1
##  2   5.8   2.7   5.1   1.9 virginica         1
##  3   7.1   3     5.9   2.1 virginica         1
##  4   6.3   2.9   5.6   1.8 virginica         1
##  5   6.5   3     5.8   2.2 virginica         1
##  6   7.6   3     6.6   2.1 virginica         1
##  7   4.9   2.5   4.5   1.7 virginica         1
##  8   7.3   2.9   6.3   1.8 virginica         1
##  9   6.7   2.5   5.8   1.8 virginica         1
## 10   7.2   3.6   6.1   2.5 virginica         1
## # … with 90 more rows

8.1.3.1 Manual Classificaiton Using Boxplot

iris_tbl2ext %>% group_by(species) %>% 
  summarize(min = quantile(sl)[1], `25%` = quantile(sl)[2], `55%` = quantile(sl)[3], `75%` = quantile(sl)[4], max = quantile(sl)[5])

## # A tibble: 2 × 6
##   species      min `25%` `55%` `75%`   max
##   <fct>      <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 versicolor   4.9  5.6    5.9   6.3   7  
## 2 virginica    4.9  6.22   6.5   6.9   7.9

By the boxplot, the value between 6.225 and 6.3 can be a candidate. So let us take 6.263.

iris_tbl2ext <- iris_tbl2ext %>% mutate(v0 = as.integer(sl > 6.263))
iris_tbl2ext

## # A tibble: 100 × 7
##       sl    sw    pl    pw species    virginica    v0
##    <dbl> <dbl> <dbl> <dbl> <fct>          <dbl> <int>
##  1   7     3.2   4.7   1.4 versicolor         0     1
##  2   6.4   3.2   4.5   1.5 versicolor         0     1
##  3   6.9   3.1   4.9   1.5 versicolor         0     1
##  4   5.5   2.3   4     1.3 versicolor         0     0
##  5   6.5   2.8   4.6   1.5 versicolor         0     1
##  6   5.7   2.8   4.5   1.3 versicolor         0     0
##  7   6.3   3.3   4.7   1.6 versicolor         0     1
##  8   4.9   2.4   3.3   1   versicolor         0     0
##  9   6.6   2.9   4.6   1.3 versicolor         0     1
## 10   5.2   2.7   3.9   1.4 versicolor         0     0
## # … with 90 more rows

8.1.3.2 Logistic Model Using `glm()` General Linear Model: Sepal Length

iris_mod1 <-iris_tbl2ext %>% glm(virginica~sl, family = binomial, .)
iris_mod1 %>% summary()

## 
## Call:
## glm(formula = virginica ~ sl, family = binomial, data = .)
## 
## Deviance Residuals: 
##      Min        1Q    Median        3Q       Max  
## -1.85340  -0.90001  -0.04717   0.96861   2.35458  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -12.5708     2.9068  -4.325 1.53e-05 ***
## sl            2.0129     0.4654   4.325 1.53e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 138.63  on 99  degrees of freedom
## Residual deviance: 110.55  on 98  degrees of freedom
## AIC: 114.55
## 
## Number of Fisher Scoring iterations: 4

iris_tbl2ext_1 <- iris_tbl2ext %>% 
  add_predictions(iris_mod1, var = "pred_1", type = "response") %>% 
  add_residuals(iris_mod1, var = "resid_1") %>%
  mutate(v1 = as.integer(pred_1 >= 0.5))
iris_tbl2ext_1  %>% arrange(desc(sl))

## # A tibble: 100 × 10
##       sl    sw    pl    pw species   virginica    v0 pred_1 resid_1    v1
##    <dbl> <dbl> <dbl> <dbl> <fct>         <dbl> <int>  <dbl>   <dbl> <int>
##  1   7.9   3.8   6.4   2   virginica         1     1  0.965  -2.33      1
##  2   7.7   3.8   6.7   2.2 virginica         1     1  0.949  -1.93      1
##  3   7.7   2.6   6.9   2.3 virginica         1     1  0.949  -1.93      1
##  4   7.7   2.8   6.7   2   virginica         1     1  0.949  -1.93      1
##  5   7.7   3     6.1   2.3 virginica         1     1  0.949  -1.93      1
##  6   7.6   3     6.6   2.1 virginica         1     1  0.939  -1.73      1
##  7   7.4   2.8   6.1   1.9 virginica         1     1  0.911  -1.32      1
##  8   7.3   2.9   6.3   1.8 virginica         1     1  0.893  -1.12      1
##  9   7.2   3.6   6.1   2.5 virginica         1     1  0.872  -0.922     1
## 10   7.2   3.2   6     1.8 virginica         1     1  0.872  -0.922     1
## # … with 90 more rows

iris_tbl2ext_1 %>% ggplot() + 
  geom_point(aes(x = sl, y = virginica, color = species)) +
  geom_line(aes(x = sl, y = pred_1))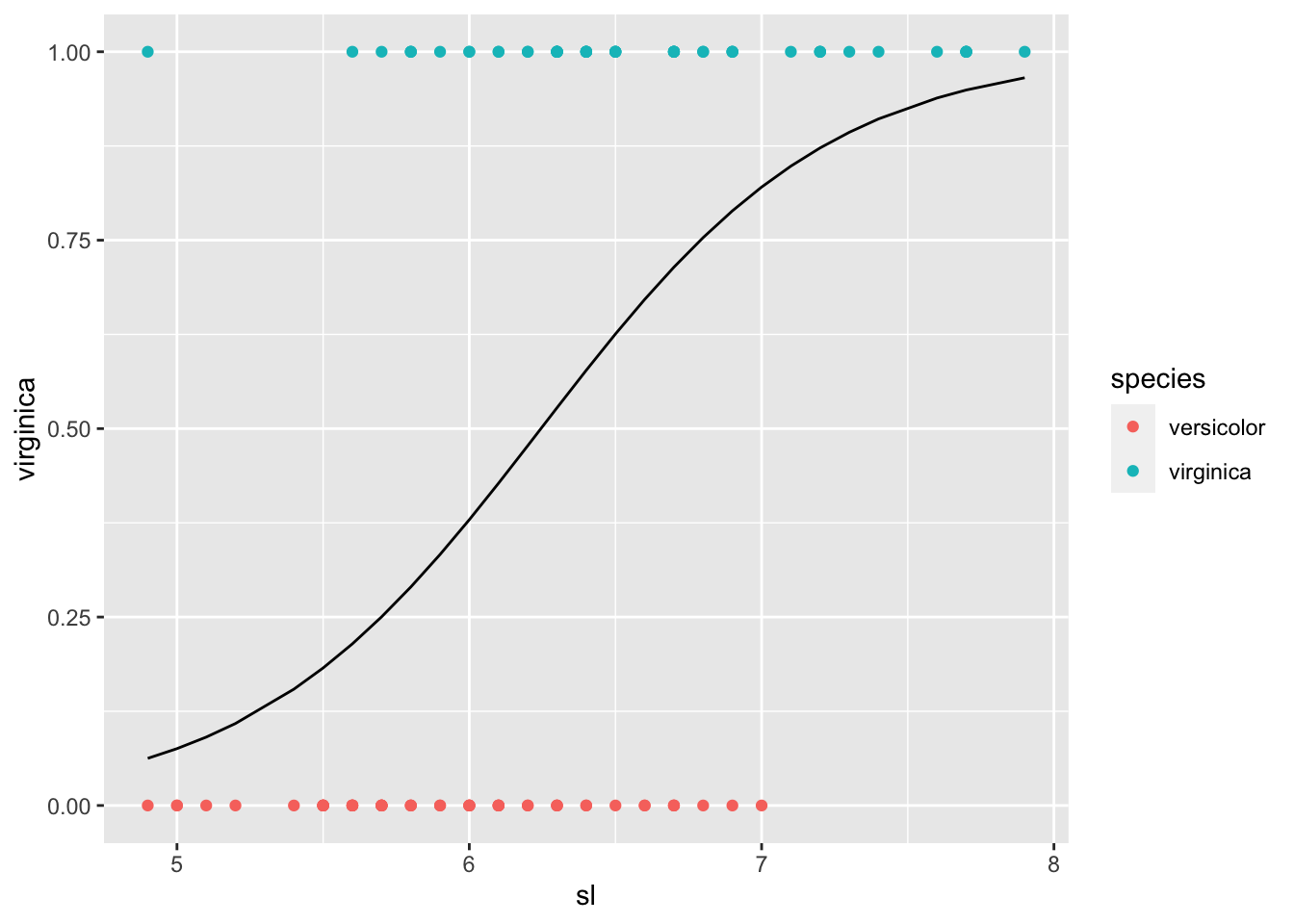

iris_tbl2ext_1 %>% filter(v0 == 1, virginica == 1) %>% nrow()/50

## [1] 0.74

iris_tbl2ext_1 %>% filter(v1 == 1, virginica == 1) %>% nrow()/50

## [1] 0.74

For both models, 74% of virginica was classified as virginica.

8.1.3.3 Confusion Matrices

iris_tbl2ext_1 %>% xtabs(~ v0 + virginica, .)

##    virginica
## v0   0  1
##   0 36 13
##   1 14 37

iris_tbl2ext_1 %>% xtabs(~ v1 + virginica, .)

##    virginica
## v1   0  1
##   0 36 13
##   1 14 37

8.1.4 Various Logistic Models

8.1.4.1 One Variable

iris_mod2 <-iris_tbl2ext %>% glm(virginica~sw, family = binomial, .)
iris_mod3 <-iris_tbl2ext %>% glm(virginica~pl, family = binomial, .)
iris_mod4 <-iris_tbl2ext %>% glm(virginica~pw, family = binomial, .)

iris_tbl2ext_one <- iris_tbl2ext_1 %>% 
  add_predictions(iris_mod2, var = "pred_2", type = "response") %>% 
  mutate(v2 = as.integer(pred_2 >= 0.5)) %>%
  add_predictions(iris_mod3, var = "pred_3", type = "response") %>% 
  mutate(v3 = as.integer(pred_3 >= 0.5)) %>%
  add_predictions(iris_mod4, var = "pred_4", type = "response") %>% 
  mutate(v4 = as.integer(pred_4 >= 0.5))
iris_tbl2ext_one  %>% arrange(desc(sl))

## # A tibble: 100 × 16
##       sl    sw    pl    pw species   virginica    v0 pred_1 resid_1    v1 pred_2
##    <dbl> <dbl> <dbl> <dbl> <fct>         <dbl> <int>  <dbl>   <dbl> <int>  <dbl>
##  1   7.9   3.8   6.4   2   virginica         1     1  0.965  -2.33      1  0.874
##  2   7.7   3.8   6.7   2.2 virginica         1     1  0.949  -1.93      1  0.874
##  3   7.7   2.6   6.9   2.3 virginica         1     1  0.949  -1.93      1  0.362
##  4   7.7   2.8   6.7   2   virginica         1     1  0.949  -1.93      1  0.462
##  5   7.7   3     6.1   2.3 virginica         1     1  0.949  -1.93      1  0.566
##  6   7.6   3     6.6   2.1 virginica         1     1  0.939  -1.73      1  0.566
##  7   7.4   2.8   6.1   1.9 virginica         1     1  0.911  -1.32      1  0.462
##  8   7.3   2.9   6.3   1.8 virginica         1     1  0.893  -1.12      1  0.515
##  9   7.2   3.6   6.1   2.5 virginica         1     1  0.872  -0.922     1  0.821
## 10   7.2   3.2   6     1.8 virginica         1     1  0.872  -0.922     1  0.665
## # … with 90 more rows, and 5 more variables: v2 <int>, pred_3 <dbl>, v3 <int>,
## #   pred_4 <dbl>, v4 <int>

iris_tbl2ext_one %>% filter(v2 == 1, virginica == 1) %>% nrow()/50

## [1] 0.62

iris_tbl2ext_one %>% filter(v3 == 1, virginica == 1) %>% nrow()/50

## [1] 0.94

iris_tbl2ext_one %>% filter(v4 == 1, virginica == 1) %>% nrow()/50

## [1] 0.92

8.1.4.2 Model Summary

msummary(list(mod1 = iris_mod1, mod2 = iris_mod2, mod3 = iris_mod3, mod4 = iris_mod3), statistic = 'p.value')

	mod1	mod2	mod3	mod4
(Intercept)	-12.571	-6.001	-43.781	-43.781
	(<0.001)	(0.004)	(<0.001)	(<0.001)
sl	2.013
	(<0.001)
sw		2.089
		(0.003)
pl			9.002	9.002
			(<0.001)	(<0.001)
Num.Obs.	100	100	100	100
AIC	114.5	132.6	37.4	37.4
BIC	119.8	137.8	42.6	42.6
Log.Lik.	-55.273	-64.290	-16.716	-16.716
RMSE	0.43	0.48	0.22	0.22

8.1.4.3 Two Variables

iris_mod12 <-iris_tbl2ext %>% glm(virginica~sl + sw, family = binomial, .)
iris_mod13 <-iris_tbl2ext %>% glm(virginica~sl + pl, family = binomial, .)
iris_mod14 <-iris_tbl2ext %>% glm(virginica~sl + pw, family = binomial, .)
iris_mod23 <-iris_tbl2ext %>% glm(virginica~sw + pl, family = binomial, .)
iris_mod24 <-iris_tbl2ext %>% glm(virginica~sw + pw, family = binomial, .)
iris_mod34 <-iris_tbl2ext %>% glm(virginica~pl + pw, family = binomial, .)

iris_tbl2ext_two <- iris_tbl2ext_one %>% 
  add_predictions(iris_mod12, var = "pred_12", type = "response") %>% 
  mutate(v12 = as.integer(pred_12 >= 0.5)) %>%
  add_predictions(iris_mod13, var = "pred_13", type = "response") %>% 
  mutate(v13 = as.integer(pred_13 >= 0.5)) %>%
  add_predictions(iris_mod14, var = "pred_14", type = "response") %>% 
  mutate(v14 = as.integer(pred_14 >= 0.5)) %>%
  add_predictions(iris_mod23, var = "pred_23", type = "response") %>% 
  mutate(v23 = as.integer(pred_23 >= 0.5)) %>%
  add_predictions(iris_mod24, var = "pred_24", type = "response") %>% 
  mutate(v24 = as.integer(pred_24 >= 0.5)) %>%
  add_predictions(iris_mod34, var = "pred_34", type = "response") %>% 
  mutate(v34 = as.integer(pred_34 >= 0.5))
iris_tbl2ext_two  %>% arrange(desc(sl))

## # A tibble: 100 × 28
##       sl    sw    pl    pw species   virginica    v0 pred_1 resid_1    v1 pred_2
##    <dbl> <dbl> <dbl> <dbl> <fct>         <dbl> <int>  <dbl>   <dbl> <int>  <dbl>
##  1   7.9   3.8   6.4   2   virginica         1     1  0.965  -2.33      1  0.874
##  2   7.7   3.8   6.7   2.2 virginica         1     1  0.949  -1.93      1  0.874
##  3   7.7   2.6   6.9   2.3 virginica         1     1  0.949  -1.93      1  0.362
##  4   7.7   2.8   6.7   2   virginica         1     1  0.949  -1.93      1  0.462
##  5   7.7   3     6.1   2.3 virginica         1     1  0.949  -1.93      1  0.566
##  6   7.6   3     6.6   2.1 virginica         1     1  0.939  -1.73      1  0.566
##  7   7.4   2.8   6.1   1.9 virginica         1     1  0.911  -1.32      1  0.462
##  8   7.3   2.9   6.3   1.8 virginica         1     1  0.893  -1.12      1  0.515
##  9   7.2   3.6   6.1   2.5 virginica         1     1  0.872  -0.922     1  0.821
## 10   7.2   3.2   6     1.8 virginica         1     1  0.872  -0.922     1  0.665
## # … with 90 more rows, and 17 more variables: v2 <int>, pred_3 <dbl>, v3 <int>,
## #   pred_4 <dbl>, v4 <int>, pred_12 <dbl>, v12 <int>, pred_13 <dbl>, v13 <int>,
## #   pred_14 <dbl>, v14 <int>, pred_23 <dbl>, v23 <int>, pred_24 <dbl>,
## #   v24 <int>, pred_34 <dbl>, v34 <int>

iris_tbl2ext_two %>% filter(v12 == 1, virginica == 1) %>% nrow()/50

## [1] 0.74

iris_tbl2ext_two %>% filter(v13 == 1, virginica == 1) %>% nrow()/50

## [1] 0.96

iris_tbl2ext_two %>% filter(v14 == 1, virginica == 1) %>% nrow()/50

## [1] 0.92

iris_tbl2ext_two %>% filter(v23 == 1, virginica == 1) %>% nrow()/50

## [1] 0.92

iris_tbl2ext_two %>% filter(v24 == 1, virginica == 1) %>% nrow()/50

## [1] 0.94

iris_tbl2ext_two %>% filter(v34 == 1, virginica == 1) %>% nrow()/50

## [1] 0.94

8.1.4.4 Model Summary

msummary(list(mod12 = iris_mod12, mod13 = iris_mod13, mod14 = iris_mod14, mod23 = iris_mod23, mod24 = iris_mod24, mod34 = iris_mod34), statistic = 'p.value')

	mod12	mod13	mod14	mod23	mod24	mod34
(Intercept)	-13.046	-39.839	-22.874	-37.058	-14.379	-45.272
	(<0.001)	(0.002)	(<0.001)	(<0.001)	(0.005)	(<0.001)
sl	1.902	-4.017	0.306
	(<0.001)	(0.013)	(0.715)
sw	0.405			-2.509	-3.907
	(0.639)			(0.184)	(0.025)
pl		13.313		9.098		5.755
		(<0.001)		(<0.001)		(0.013)
pw			12.845		15.700	10.447
			(<0.001)		(<0.001)	(0.005)
Num.Obs.	100	100	100	100	100	100
AIC	116.3	29.9	39.3	37.5	33.4	26.6
BIC	124.1	37.7	47.1	45.3	41.2	34.4
Log.Lik.	-55.163	-11.925	-16.643	-15.756	-13.700	-10.282
RMSE	0.43	0.18	0.22	0.22	0.21	0.19

8.1.4.5 Three and All Variables

iris_mod123 <-iris_tbl2ext %>% glm(virginica~sl + sw + pl, family = binomial, .)
iris_mod124 <-iris_tbl2ext %>% glm(virginica~sl + sw + pw, family = binomial, .)
iris_mod134 <-iris_tbl2ext %>% glm(virginica~sl + pl + pw, family = binomial, .)
iris_mod234 <-iris_tbl2ext %>% glm(virginica~sw + pl + pw, family = binomial, .)

## Warning: glm.fit: 数値的に 0 か 1 である確率が生じました

iris_mod1234 <-iris_tbl2ext %>% glm(virginica~sl + sw + pl + pw, family = binomial, .)

iris_tbl2ext_all <- iris_tbl2ext_two %>% 
  add_predictions(iris_mod123, var = "pred_123", type = "response") %>% 
  mutate(v123 = as.integer(pred_123 >= 0.5)) %>%
  add_predictions(iris_mod124, var = "pred_124", type = "response") %>% 
  mutate(v124 = as.integer(pred_124 >= 0.5)) %>%
  add_predictions(iris_mod134, var = "pred_134", type = "response") %>% 
  mutate(v134 = as.integer(pred_134 >= 0.5)) %>%
  add_predictions(iris_mod234, var = "pred_234", type = "response") %>% 
  mutate(v234 = as.integer(pred_234 >= 0.5)) %>%
  add_predictions(iris_mod1234, var = "pred_1234", type = "response") %>% 
  mutate(v1234 = as.integer(pred_1234 >= 0.5)) 
iris_tbl2ext_all  %>% arrange(desc(sl))

## # A tibble: 100 × 38
##       sl    sw    pl    pw species   virginica    v0 pred_1 resid_1    v1 pred_2
##    <dbl> <dbl> <dbl> <dbl> <fct>         <dbl> <int>  <dbl>   <dbl> <int>  <dbl>
##  1   7.9   3.8   6.4   2   virginica         1     1  0.965  -2.33      1  0.874
##  2   7.7   3.8   6.7   2.2 virginica         1     1  0.949  -1.93      1  0.874
##  3   7.7   2.6   6.9   2.3 virginica         1     1  0.949  -1.93      1  0.362
##  4   7.7   2.8   6.7   2   virginica         1     1  0.949  -1.93      1  0.462
##  5   7.7   3     6.1   2.3 virginica         1     1  0.949  -1.93      1  0.566
##  6   7.6   3     6.6   2.1 virginica         1     1  0.939  -1.73      1  0.566
##  7   7.4   2.8   6.1   1.9 virginica         1     1  0.911  -1.32      1  0.462
##  8   7.3   2.9   6.3   1.8 virginica         1     1  0.893  -1.12      1  0.515
##  9   7.2   3.6   6.1   2.5 virginica         1     1  0.872  -0.922     1  0.821
## 10   7.2   3.2   6     1.8 virginica         1     1  0.872  -0.922     1  0.665
## # … with 90 more rows, and 27 more variables: v2 <int>, pred_3 <dbl>, v3 <int>,
## #   pred_4 <dbl>, v4 <int>, pred_12 <dbl>, v12 <int>, pred_13 <dbl>, v13 <int>,
## #   pred_14 <dbl>, v14 <int>, pred_23 <dbl>, v23 <int>, pred_24 <dbl>,
## #   v24 <int>, pred_34 <dbl>, v34 <int>, pred_123 <dbl>, v123 <int>,
## #   pred_124 <dbl>, v124 <int>, pred_134 <dbl>, v134 <int>, pred_234 <dbl>,
## #   v234 <int>, pred_1234 <dbl>, v1234 <int>

iris_tbl2ext_all %>% filter(v123 == 1, virginica == 1) %>% nrow()/50

## [1] 0.96

iris_tbl2ext_all %>% filter(v124 == 1, virginica == 1) %>% nrow()/50

## [1] 0.96

iris_tbl2ext_all %>% filter(v134 == 1, virginica == 1) %>% nrow()/50

## [1] 0.98

iris_tbl2ext_all %>% filter(v234 == 1, virginica == 1) %>% nrow()/50

## [1] 0.98

iris_tbl2ext_all %>% filter(v1234 == 1, virginica == 1) %>% nrow()/50

## [1] 0.98

8.1.4.6 Confusion Matrices

iris_tbl2ext_all %>% xtabs(~ v134 + virginica, .)

##     virginica
## v134  0  1
##    0 48  1
##    1  2 49

iris_tbl2ext_all %>% xtabs(~ v234 + virginica, .)

##     virginica
## v234  0  1
##    0 48  1
##    1  2 49

iris_tbl2ext_all %>% xtabs(~ v1234 + virginica, .)

##      virginica
## v1234  0  1
##     0 49  1
##     1  1 49

8.1.4.7 Model Summary

msummary(list(mod123 = iris_mod123, mod124 = iris_mod124, mod134 = iris_mod134, mod234 = iris_mod234, mod1234 = iris_mod1234), statistic = 'p.value')

	mod123	mod124	mod134	mod234	mod1234
(Intercept)	-38.215	-20.287	-40.831	-50.527	-42.638
	(0.007)	(0.012)	(0.028)	(0.035)	(0.097)
sl	-3.852	1.295	-3.839		-2.465
	(0.024)	(0.234)	(0.071)		(0.303)
sw	-0.639	-4.823		-8.376	-6.681
	(0.780)	(0.021)		(0.079)	(0.136)
pl	13.147		9.754	7.875	9.429
	(<0.001)		(0.029)	(0.040)	(0.047)
pw		15.923	10.102	21.430	18.286
		(<0.001)	(0.028)	(0.045)	(0.061)
Num.Obs.	100	100	100	100	100
AIC	31.8	33.9	23.5	21.3	21.9
BIC	42.2	44.3	33.9	31.7	34.9
Log.Lik.	-11.886	-12.951	-7.746	-6.633	-5.949
RMSE	0.18	0.20	0.16	0.15	0.14

iris_tbl2ext_all %>% select(virginica, v0, v1, v2, v3, v4, v12, v13, v14, v23, v24, v34, v123, v124, v134, v234, v1234)

## # A tibble: 100 × 17
##    virginica    v0    v1    v2    v3    v4   v12   v13   v14   v23   v24   v34
##        <dbl> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int>
##  1         0     1     1     1     0     0     1     0     0     0     0     0
##  2         0     1     1     1     0     0     1     0     0     0     0     0
##  3         0     1     1     1     1     0     1     0     0     0     0     0
##  4         0     0     0     0     0     0     0     0     0     0     0     0
##  5         0     1     1     0     0     0     1     0     0     0     0     0
##  6         0     0     0     0     0     0     0     0     0     0     0     0
##  7         0     1     1     1     0     0     1     0     0     0     0     0
##  8         0     0     0     0     0     0     0     0     0     0     0     0
##  9         0     1     1     1     0     0     1     0     0     0     0     0
## 10         0     0     0     0     0     0     0     0     0     0     0     0
## # … with 90 more rows, and 5 more variables: v123 <int>, v124 <int>,
## #   v134 <int>, v234 <int>, v1234 <int>

8.2 Conclusions

8.2.1 Hypothesis generation vs. hypothesis confirmation

Each observation can either be used for exploration or confirmation, not both.
You can use an observation as many times as you like for exploration, but you can only use it once for confirmation. As soon as you use an observation twice, you’ve switched from confirmation to exploration.

If you are serious about doing an confirmatory analysis, one approach is to split your data into three pieces before you begin the analysis:

60% of your data goes into a training (or exploration) set. You’re allowed to do anything you like with this data: visualise it and fit tons of models to it.
20% goes into a query set. You can use this data to compare models or visualisations by hand, but you’re not allowed to use it as part of an automated process.
20% is held back for a test set. You can only use this data ONCE, to test your final model.

8.2.2 References

Iris Classification: https://github.com/trevorwitter/Iris-classification-R

Chapter 8 Topics in Exploratory Data Analysis II

Project

8.1 Classification IRIS dataset

8.1.1 Setup

8.1.2 Data: iris

8.1.2.1 Visualization

8.1.2.2 Sepal Length

8.1.3 Binary classification

8.1.3.1 Manual Classificaiton Using Boxplot

8.1.3.2 Logistic Model Using glm() General Linear Model: Sepal Length

8.1.3.3 Confusion Matrices

8.1.4 Various Logistic Models

8.1.4.1 One Variable

8.1.4.2 Model Summary

8.1.4.3 Two Variables

8.1.4.4 Model Summary

8.1.4.5 Three and All Variables

8.1.4.6 Confusion Matrices

8.1.4.7 Model Summary

8.2 Conclusions

8.2.1 Hypothesis generation vs. hypothesis confirmation

8.2.2 References

Chapter 8 Topics in Exploratory Data Analysis II　

8.1.2 Data: `iris`

8.1.3.2 Logistic Model Using `glm()` General Linear Model: Sepal Length