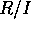 が、整域や体となるイデアル I の満たすべき条件を考える。
が、整域や体となるイデアル I の満たすべき条件を考える。
R を可換環、I をイデアルとする。このとき、剰余環 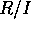 が、整域や体となるイデアル I の満たすべき条件を考える。
が、整域や体となるイデアル I の満たすべき条件を考える。

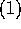
 が整域であることは、以下のことと同値である。
が整域であることは、以下のことと同値である。

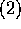 命題
命題 ![]() により、
により、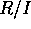 が体であることと、
が体であることと、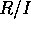 の 0 でないイデアルは、
の 0 でないイデアルは、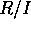 のみであることは同値である。これは、言い換えると、R のイデアル J で I を真に含むものは、R に限られるということと同値であるから(練習問題参照)、I が R の極大イデアルであることと同値である。
のみであることは同値である。これは、言い換えると、R のイデアル J で I を真に含むものは、R に限られるということと同値であるから(練習問題参照)、I が R の極大イデアルであることと同値である。
 I:極大イデアル
I:極大イデアル 
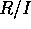 :体
:体 
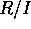 :整域
:整域  I:素イデアル。
I:素イデアル。
R を可換環とすると、上の定理から、零イデアル  が素イデアルであることと、R が整域であることが同値であり、また、
が素イデアルであることと、R が整域であることが同値であり、また、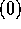 が極大イデアルであることと、R が体であることが同値である。
が極大イデアルであることと、R が体であることが同値である。
定理 ![]() により、極大イデアルは、常に素イデアルだから、
により、極大イデアルは、常に素イデアルだから、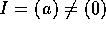 を素イデアルとして、I が極大イデアルであることを示す。J を I を真に含む R のイデアルとする。R は、単項イデアル整域だから、
を素イデアルとして、I が極大イデアルであることを示す。J を I を真に含む R のイデアルとする。R は、単項イデアル整域だから、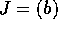 とおける。
とおける。 だから、a = bc となる
だから、a = bc となる 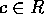 が存在する。
が存在する。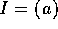 は、素イデアルだから
は、素イデアルだから 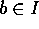 または
または  。
。 とすると、
とすると、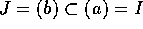 となり J が I を真に含むイデアルであることに反するから、
となり J が I を真に含むイデアルであることに反するから、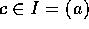 。すなわち、c = ad となる
。すなわち、c = ad となる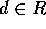 が存在する。これより、
が存在する。これより、
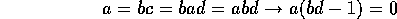
を得る。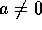 だったから bd = 1 すなわち
だったから bd = 1 すなわち  となり J = R となるから、I は極大イデアルである。
となり J = R となるから、I は極大イデアルである。
まず、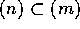 は、
は、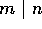 と同値であることに注意する。これより、
と同値であることに注意する。これより、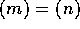 であることと、
であることと、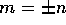 は同値であることが分かる。さて、「
は同値であることが分かる。さて、「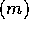 が極大であること」と、「
が極大であること」と、「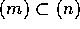 ならば、
ならば、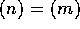 または
または 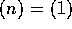 であること」とは、同値である。これより、n の約数は、
であること」とは、同値である。これより、n の約数は、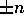 であるか、または
であるか、または 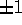 であるかのどちらかであることを得る。極大イデアルは、
であるかのどちらかであることを得る。極大イデアルは、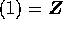 とは異なるから、
とは異なるから、
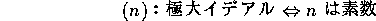
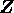 は、単項イデアル整域であるから、命題
は、単項イデアル整域であるから、命題 ![]() より、零でないイデアルが極大イデアルであることと、素イデアルであることは、同値であることが分かる。
より、零でないイデアルが極大イデアルであることと、素イデアルであることは、同値であることが分かる。
この命題により、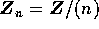 が体であることと、整域であることと、n が素数であることは、全て同値であることもわかった。
が体であることと、整域であることと、n が素数であることは、全て同値であることもわかった。

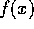 が定数の時は、上の3つのどの条件も満たさないから考えなくて良い。そこで、
が定数の時は、上の3つのどの条件も満たさないから考えなくて良い。そこで、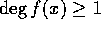 とする。
とする。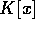 は、単項イデアル整域であるから、
は、単項イデアル整域であるから、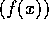 が極大イデアルであることと、素イデアルであることは、同値である。このことと、
が極大イデアルであることと、素イデアルであることは、同値である。このことと、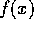 が既約であることが同値であることを示す。
が既約であることが同値であることを示す。
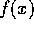 を可約とする。すなわち、
を可約とする。すなわち、 、
、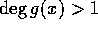 、
、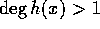 とする。すると、
とする。すると、
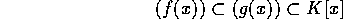
でどちらも等号は成り立たない。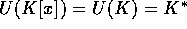 だから、練習問題より以下が同値であることから明か。
だから、練習問題より以下が同値であることから明か。

逆に、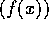 は極大イデアルではないとする。
は極大イデアルではないとする。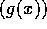 を
を 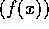 を真に含みかつ
を真に含みかつ 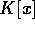 とは異なるイデアルとする。すると、
とは異なるイデアルとする。すると、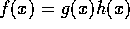 とかけ、条件から、
とかけ、条件から、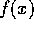 は、可約であることが分かる。
は、可約であることが分かる。

次数の高い多項式について、既約かどうかはどのように判定すればよいのだろうか。実は、一般には非常に難しい。しかし、次の判定法は有効である。
可約として矛盾を導く。
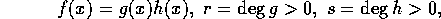
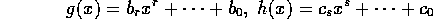
とする。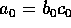 は仮定より p で割り切れるが、
は仮定より p で割り切れるが、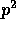 では割り切れない。従って、p は、
では割り切れない。従って、p は、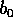 は割らないが、
は割らないが、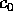 は割ると仮定する。一方、
は割ると仮定する。一方、 は仮定から p で割れないから、
は仮定から p で割れないから、 も p で割れない。
も p で割れない。 は p で割れるとしているから、今 i を
は p で割れるとしているから、今 i を 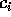 が p で割り切れない最小の整数とする。従って、
が p で割り切れない最小の整数とする。従って、
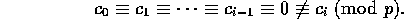
すると、
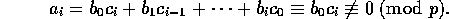
である。仮定から  となり、これは、矛盾である。従って、
となり、これは、矛盾である。従って、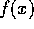 は既約である。
は既約である。
この命題は、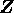 上既約かどうかの判定法であるが、実は、練習問題にもあるように、ガウスの補題(命題
上既約かどうかの判定法であるが、実は、練習問題にもあるように、ガウスの補題(命題 ![]() )といわれるものにより
)といわれるものにより 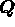 上既約であることも分かる。
上既約であることも分かる。
例えば、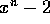 、
、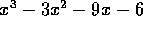 は、
は、 上(そして、
上(そして、 上)既約である。
上)既約である。