

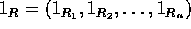 、
、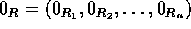 である。
である。
また、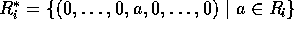 (第 i 成分以外は、0)とすると、
(第 i 成分以外は、0)とすると、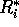 は、R の両側イデアルである。
は、R の両側イデアルである。
可換環 R の二つのイデアル I,J が I+J = R を満たすとき、I は J と互いに素であるという。すなわち次の同値条件を満たすことである。
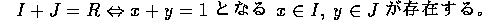
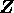 においては、
においては、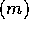 と
と 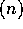 が互いに素な事と、
が互いに素な事と、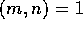 すなわち、m と n の最大公約数が 1 であることは同値である。実際、x+y = 1 となる
すなわち、m と n の最大公約数が 1 であることは同値である。実際、x+y = 1 となる 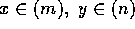 が存在するということは、am+bn = 1 となる
が存在するということは、am+bn = 1 となる 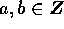 が存在することであり、このことは、
が存在することであり、このことは、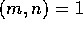 と同値であるからである。
と同値であるからである。
「3 で割って 1 余り、10 で割って 3 余り、7 では割り切れ、13 で割ると 11 余るような数はあるだろうか。またあるならばそれをすべて求めることが出来るか。」という種類の問題は、古くからいろいろと考えられていたようで孫子の「兵法」に軍隊の編成の問題から議論されていることなどから、この問題を取り扱った次の定理は中国剰余定理 (Chinise Remainer's Theorem) と呼ばれているとのことである。
n = 2 のとき 仮定より、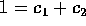 となる
となる 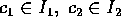 がある。そこで、
がある。そこで、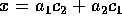 とおくと、
とおくと、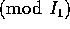 で、
で、
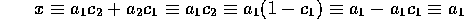
となる。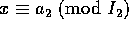 も同様にして得る。
も同様にして得る。
n > 2 のとき まず、各 i について、次の性質を満たす 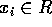 が存在することを示す。
が存在することを示す。
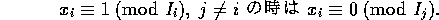
記号を見やすくするため、i = 1 のときを考える。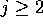 については、
については、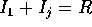 だから、
だから、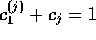 となる、
となる、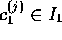 、
、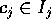 がある。すべてを掛け合わせると、
がある。すべてを掛け合わせると、
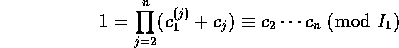
だから、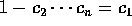 とおくと、
とおくと、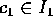 である。とくに、
である。とくに、
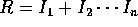 すなわち、二つのイデアル
すなわち、二つのイデアル 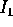 、
、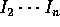 は互いに素であることが分かる。上記 n=2 の時は、既に示してあるから、
は互いに素であることが分かる。上記 n=2 の時は、既に示してあるから、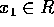 で、
で、
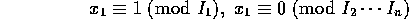
を満たすものが存在することが分かる。ところが、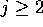 に対して、
に対して、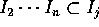 であるから、
であるから、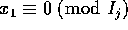 でもある。これで最初の主張が示された。
でもある。これで最初の主張が示された。
今、各 i について、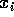 をとり、
をとり、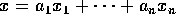 とおくと、
とおくと、
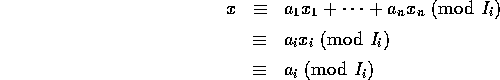
となり、求めるものが得られた。