 を商体とする。
を商体とする。
ここでは、R を一意分解整域、 を商体とする。
を商体とする。
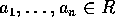 の最大公約元であるとは、以下の2条件を満たすことである。
の最大公約元であるとは、以下の2条件を満たすことである。
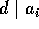 ,
, 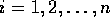 。
。
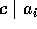 ,
, 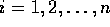 ならば、
ならば、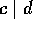 。
。
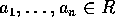 の最小公倍元であるとは、以下の2条件を満たすことである。
の最小公倍元であるとは、以下の2条件を満たすことである。
 ,
, 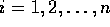 。
。
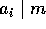 ,
,  ならば、
ならば、 。
。
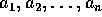 の最大公約元が 1 であるとき、
の最大公約元が 1 であるとき、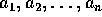 は、互いに素 (coprime) であるという。
は、互いに素 (coprime) であるという。
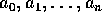 が互いに素である時、
が互いに素である時、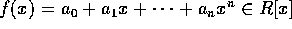 を原始多項式 (primitive polynomial) という。
を原始多項式 (primitive polynomial) という。
練習問題にもあるように、R が一意分解整域ならば最大公約元、最小公倍元は存在する。
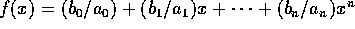 、
、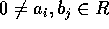 。m を
。m を  の最小公倍元、
の最小公倍元、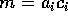 、d を
、d を 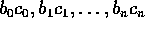 の最大公約元、
の最大公約元、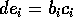 とする。
とする。 は互いに素である。さらに、
は互いに素である。さらに、
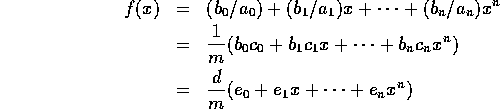
ここで、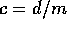 、
、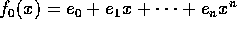 とおけばよい。
とおけばよい。
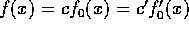 、
、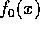 、
、 は、R 上の原始多項式、
は、R 上の原始多項式、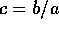 、
、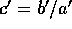 、a と b、
、a と b、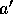 と
と 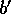 は互いに素な R の元とする。
は互いに素な R の元とする。
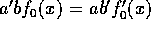 だから、それぞれの係数の最大公約元を考えると、最大公約元は、正則元倍をのぞいて、一意に決まり、
だから、それぞれの係数の最大公約元を考えると、最大公約元は、正則元倍をのぞいて、一意に決まり、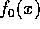 、
、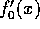 はともに原始多項式だから、
はともに原始多項式だから、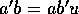 となる
となる  がある。従って、
がある。従って、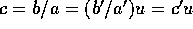 。
。
K の2元  について、
について、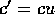 となる
となる  が存在するとき、
が存在するとき、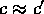 と書く。このとき、
と書く。このとき、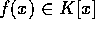 について、
について、
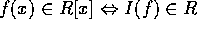 。
。
 。
。
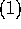
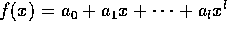 、
、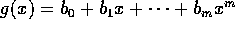 を原始多項式、
を原始多項式、
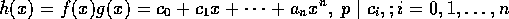
p は素元、とする。 のうち、p で割れない最小の i を
のうち、p で割れない最小の i を 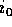 とする。また、
とする。また、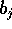 のうち、p で割れない最小の j を
のうち、p で割れない最小の j を 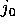 とする。すると、
とする。すると、
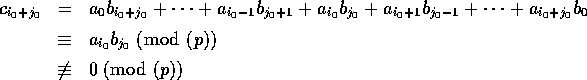
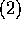
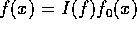 、
、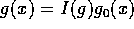 で、
で、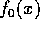 、
、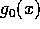 は原始多項式と書く。すると、
は原始多項式と書く。すると、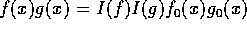 で、
で、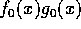 は、
は、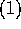 より、原始多項式だから、
より、原始多項式だから、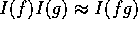 。
。
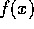 が
が  の元として既約ならば、
の元として既約ならば、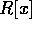 の元として既約であることは明らか。
の元として既約であることは明らか。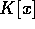 において、
において、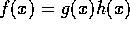 、
、 とする。ここで、
とする。ここで、 、
、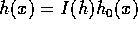 、
、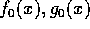 は原始多項式とすると、
は原始多項式とすると、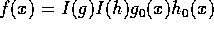 、
、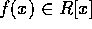 より、
より、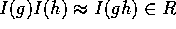 。従って、
。従って、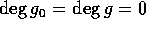 又は、
又は、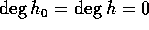 。従って、
。従って、 においても既約である。
においても既約である。
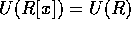 である事に注意すると、かつ上の
である事に注意すると、かつ上の 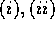 が素元であることは明か。
が素元であることは明か。
逆に 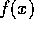 を素元とする。f = gh とすると、g, h のいずれかは、
を素元とする。f = gh とすると、g, h のいずれかは、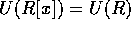 の元だから、
の元だから、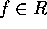 又は、同じことだが
又は、同じことだが 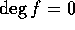 ならば、f は、R の素元である。
ならば、f は、R の素元である。 ならば、f は既約で、かつ
ならば、f は既約で、かつ 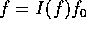 より
より 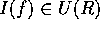 となり f は原始多項式。従って、この場合は、
となり f は原始多項式。従って、この場合は、 が成立する。
が成立する。
定理 ![]() の証明
の証明
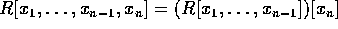 だから、n = 1 の場合、すなわち、R が一意分解整域の時、
だから、n = 1 の場合、すなわち、R が一意分解整域の時、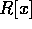 が一意分解整域であることを示せばよい。
が一意分解整域であることを示せばよい。
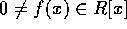 が素元分解可能であることを
が素元分解可能であることを  に関する帰納法で示す。
に関する帰納法で示す。 の時は、R が一意分解整域であるから、補題
の時は、R が一意分解整域であるから、補題 ![]()
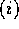 に注意すれば
に注意すれば 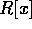 の素元に分解できることが分かる。
の素元に分解できることが分かる。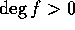 かつ可約の時は、f = gh、
かつ可約の時は、f = gh、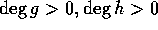 と表すと、
と表すと、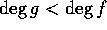 、
、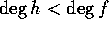 だから、帰納法の仮定により、g、h ともに素元分解できる。従って、f も素元分解できる。そこで既約とする。すると、
だから、帰納法の仮定により、g、h ともに素元分解できる。従って、f も素元分解できる。そこで既約とする。すると、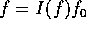 、
、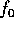 は原始多項式と書くと、
は原始多項式と書くと、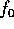 は既約でもあるから、補題
は既約でもあるから、補題 ![]()
 により素元、後は、
により素元、後は、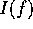 に R における素元分解を適用すれば
に R における素元分解を適用すれば 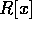 における素元分解が得られる。
における素元分解が得られる。
一意性:
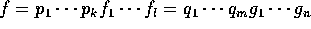 を f の素元分解とし、
を f の素元分解とし、
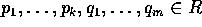 、
、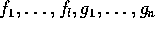 は次数が 1 以上の既約原始多項式とする。すると、
は次数が 1 以上の既約原始多項式とする。すると、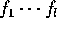 、
、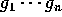 は 補題
は 補題 ![]() により、ともに原始多項式だから、
により、ともに原始多項式だから、
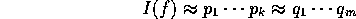
を得、ある 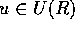 によって、
によって、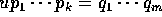 と書けるから、R が一意分解整域であることより、この部分の一意性は得られる。一方、
と書けるから、R が一意分解整域であることより、この部分の一意性は得られる。一方、
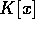 は、体上の多項式環だからユークリッド整域、とくに一意分解整域で
は、体上の多項式環だからユークリッド整域、とくに一意分解整域で 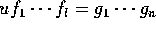 に一意性を適用すると、適当に順番を入れ替えると、
に一意性を適用すると、適当に順番を入れ替えると、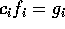 、
、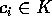 と書くことが出来る。
と書くことが出来る。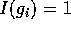 だから
だから 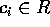 を得、
を得、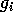 が原始多項式であることより、
が原始多項式であることより、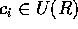 を得る。従って、分解は一意的である。
を得る。従って、分解は一意的である。