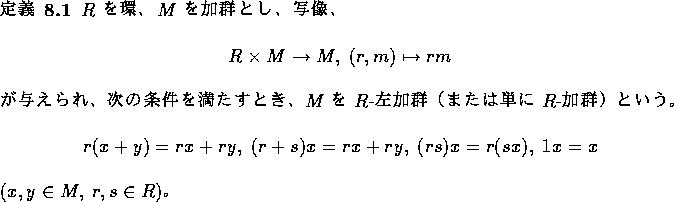
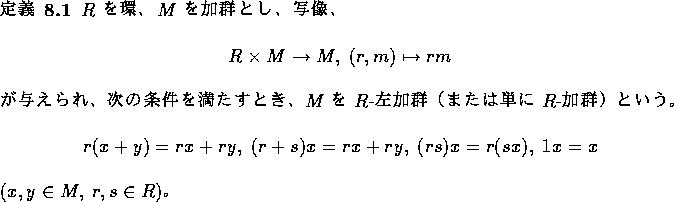
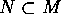 が R-部分加群であるとは、N が 部分加群で、かつ、
が R-部分加群であるとは、N が 部分加群で、かつ、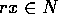 がすべての、
がすべての、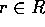 、
、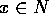 が成り立つことを言う。
が成り立つことを言う。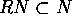 なる条件を N が R の作用で閉じているとか安定であるとも言う。
なる条件を N が R の作用で閉じているとか安定であるとも言う。
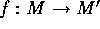 が R-加群の準同型であるとは、
が R-加群の準同型であるとは、
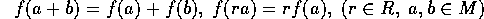
を満たす時を言う。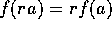 なる条件を、f は、R の作用と可換などとも言う。
なる条件を、f は、R の作用と可換などとも言う。



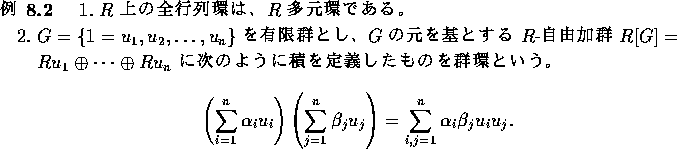
G を有限群、 、V を A-加群とする。
、V を A-加群とする。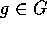 のとき
のとき 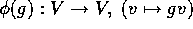 とすると、
とすると、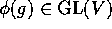 、また、
、また、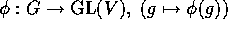 は、群としての準同型である。逆に、群の準同型
は、群としての準同型である。逆に、群の準同型 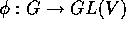 が与えられると、V は、A 加群となる。
が与えられると、V は、A 加群となる。
M を R-加群とする。M が 0 と M 以外に部分加群を持たないとき、M を既約と言う。既約でないとき、可約と言う。
f を R-準同型とすると、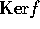 、
、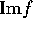 は、共に R-部分加群である。
は、共に R-部分加群である。
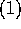
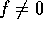 とすると、
とすると、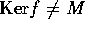 、
、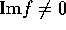 だから
だから 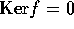 、
、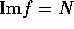 となる。これは、f が同型写像であることを意味する。
となる。これは、f が同型写像であることを意味する。
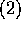
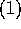 より明か。
より明か。