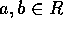 とする。
とする。
R を整域、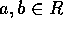 とする。
とする。
 となる
となる 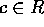 がある。このとき、
がある。このとき、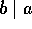 と書く。
と書く。
 となる
となる 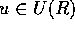 がある。このとき、
がある。このとき、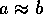 と書き同伴という。
と書き同伴という。
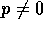 が正則元でなくかつ、
が正則元でなくかつ、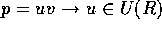 又は、
又は、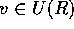 の時、p を素元という。
の時、p を素元という。

 p = ab とする。仮定より、
p = ab とする。仮定より、 または
または 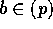 。
。 とする。
とする。
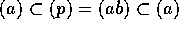 だから、
だから、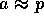 で p = au、
で p = au、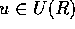 と書ける。
と書ける。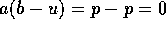 で、R は整域だから
で、R は整域だから  。
。
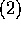 p を素数とする。
p を素数とする。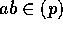 とすると、a または
とすると、a または 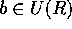 のときは明らか。
ab = pc、
のときは明らか。
ab = pc、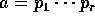 、
、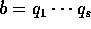 、
、 を素元分解とする。
を素元分解とする。
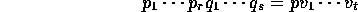
素元分解の一意性より 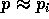 又は
又は  。そこで、
。そこで、
 とすると、
とすると、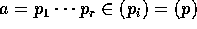 。
。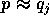 とすると、
とすると、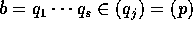 。
。
この命題は、ある環 R が一意分解整域ではないことを示すためにも用いられる。すなわち、素元ではあるが、それで生成されたイデアルが、素イデアルではない元の存在が示されればそれで良い。
命題 ![]() により
により  、また、命題
、また、命題 ![]() により
により  も示してあるから、
も示してあるから、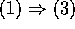 を示せばよい。
を示せばよい。
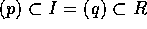 とすると、p = qa と書ける。仮定より、q が単元か、a が単元。それぞれ、
とすると、p = qa と書ける。仮定より、q が単元か、a が単元。それぞれ、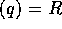 または、
または、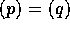 となる。従って、
となる。従って、 は極大イデアルである。
は極大イデアルである。
R を単項イデアル整域とし、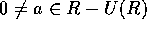 とする。このとき、
とする。このとき、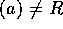 だから
だから 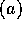 を含む極大イデアル
を含む極大イデアル 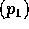 が存在する。命題
が存在する。命題 ![]() より
より 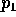 は素元である。
は素元である。
 より、
より、 と表すことが出来、
と表すことが出来、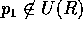 より、
より、 は、
は、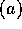 を真に含む。
を真に含む。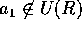 ならば素元
ならば素元  が存在して、
が存在して、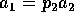 、(
、( ) と書くことが出来る。この様にして順に
) と書くことが出来る。この様にして順に 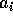 を取っていくとき、正則元でない限りにおいて、真に増加する列
を取っていくとき、正則元でない限りにおいて、真に増加する列

がつくれる。
 は R のイデアルだから、
は R のイデアルだから、 と書ける。従って、ある i について、
と書ける。従って、ある i について、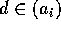 となるから、
となるから、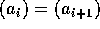 となり真に増加することはない。よってある r について
となり真に増加することはない。よってある r について 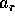 は正則元、すなわち、
は正則元、すなわち、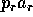 は素元で、
は素元で、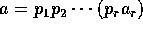 。
。
一意性:
 、
、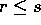 とし、r に関する帰納法を用いる。
とし、r に関する帰納法を用いる。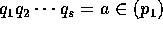 で、
で、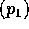 は素イデアルだから、
は素イデアルだから、 となる i がある。しかし、
となる i がある。しかし、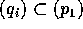 で、どちらも極大イデアルであるから、
で、どちらも極大イデアルであるから、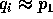 である。番号を付け替え、
である。番号を付け替え、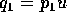 、
、 とすると、
とすると、

を得るから、 。帰納法により、r = s かつ、番号の付け替えにより、
。帰納法により、r = s かつ、番号の付け替えにより、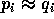 となることが分かる。
となることが分かる。
これにより、ユークリッド整域は、単項イデアル整域であり、単項イデアル整域は、一意分解整域であることが分かった。しかし、これだけでは、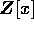 や、
や、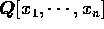 が一意分解整域かどうかは分からない。
が一意分解整域かどうかは分からない。
