
この節では、可換環に逆元をつけ加えてどれぐらい体に近く出来るかを考える。

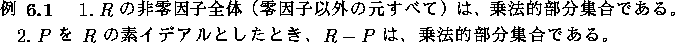
R を可換環 S を乗法的部分集合とする。
 に次のような関係を定義する。
に次のような関係を定義する。
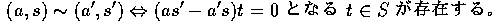
すると、これは同値関係になる。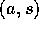 を含む同値類を
を含む同値類を 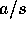 で表し、同値類全体を
で表し、同値類全体を 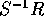 で表す。
で表す。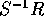 に加法と、乗法を次のように定義する。
に加法と、乗法を次のように定義する。
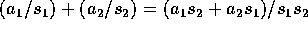
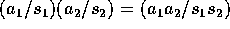
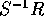 の表し方によらず、一意的に定まり、可換環になる。これをR の S による商環 (quotient ring) という。
の表し方によらず、一意的に定まり、可換環になる。これをR の S による商環 (quotient ring) という。
 、
、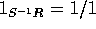 、
、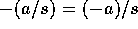 であり、
であり、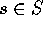 ならば、
ならば、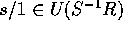 である。
である。
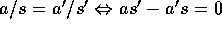 。
。
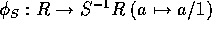 を自然な準同型という。
を自然な準同型という。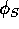 :単射
:単射  S は、零因子を含まない。
S は、零因子を含まない。


体は、 がただ一つの極大イデアルであるから、局所環である。
がただ一つの極大イデアルであるから、局所環である。
R を局所環、M をその極大イデアルとする。I を R とは異なるイデアルとすると、Zorn の補題を用いることにより、I を含む極大イデアルが一つ存在する。R は、局所環であるから 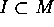 であることが分かる。すなわち、M は、R の真のイデアルをすべて含む。
であることが分かる。すなわち、M は、R の真のイデアルをすべて含む。
 M を R のただ一つの極大イデアルとする。
M を R のただ一つの極大イデアルとする。 だから、
だから、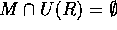 すなわち、
すなわち、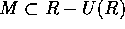 。ここで、
。ここで、 とすると、
とすると、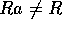 だから、
だから、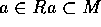 。よって、
。よって、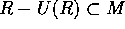 。従って、
。従って、 であり、これはイデアルである。
であり、これはイデアルである。
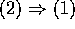 J を
J を 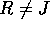 なる R のイデアル、
なる R のイデアル、 とする。このとき、
とする。このとき、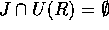 だから、
だから、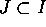 。よって I は R のただ一つの極大イデアルである。
。よって I は R のただ一つの極大イデアルである。

 は、
は、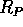 のイデアルである。
のイデアルである。
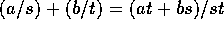 、
、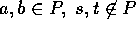 とすると、
とすると、 、
、 だから、
だから、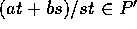 。同様に、
。同様に、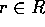 の時、
の時、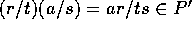 。従って、
。従って、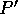 は
は 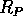 のイデアルである。
のイデアルである。
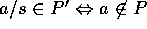 .
.
(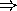 )
) 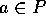 ならば、
ならば、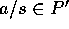 だから、明らか。
だから、明らか。
(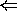 )
)  とすると、
とすると、 となる
となる 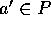 、
、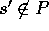 が存在する。従って、
が存在する。従って、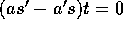 を満たす
を満たす 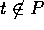 が存在する。これより、
が存在する。これより、 だから、仮定より
だから、仮定より  を得る。
を得る。

(`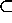 ' であること。)
' であること。)  とすると、
とすると、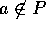 だから、
だから、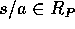 。すなわち、
。すなわち、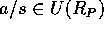 。
。
(` ' であること。)
' であること。) 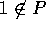 だから、
だから、 。
。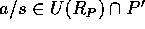 とすると、
とすると、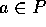 であり、かつ、
であり、かつ、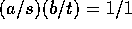 となる、
となる、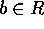 、
、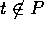 が存在する。これより、ある
が存在する。これより、ある  により、
により、 となるが、この式の右辺は、P に属さず、左辺は、P に属することになり矛盾。従って、
となるが、この式の右辺は、P に属さず、左辺は、P に属することになり矛盾。従って、 。これより、
。これより、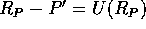 を得る。
を得る。