R-加群 M がネーター加群だとする。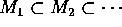
を部分加群の列とすると、
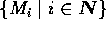の中に極大なもの 
が存在するから、
。逆に、空でない部分加群の族 S に極大なものが無ければ、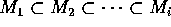
を真に増大する鎖として取る。すると、
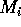は S の中で極大ではないから、
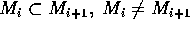となるものを含む、これを続けていくと、真に増大する部分加群の無限列がとれるので昇鎖律を満たさない。
アルチン加群であることと、降鎖律を満たすことが同値であることの証明も同様。
N を M の部分 R-加群、S を N の R-部分加群で、R-有限生成なもの全体とする。仮定から、S に極大元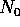 
が存在する。
ならば、
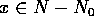とすると、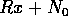
は、有限生成でかつ 
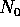を真に含むことになり 
の極大性に反するから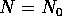 
、すなわち、N も有限生成である。
を M の部分加群の列とする。
は、R-加群だから、仮定より有限生成で、
となる生成元があり、N の仮定よりある 
にすべての 
が入る。従って、
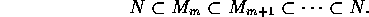
よって、M は昇鎖律を満たす。命題 
により M はネーター加群である。
任意のイデアルは、1 個の元で生成されるから、明らか。
n=1 の時を示せばよい。I を 
のイデアルとする。
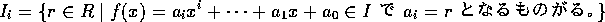
とおくと、これは R のイデアルである。また、
ならば、
だから、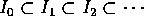
である。仮定より、R はネーター環で、命題 より昇鎖律を満たすから
となる r が存在する。命題 により、各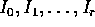 
は有限生成だから、
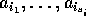を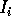 
の R 上の生成元とする。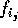
を最高次の係数が、
となるI の i 次多項式とする。このとき、これらが I を生成すること、すなわち次が成立することを示す。
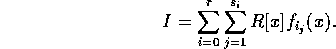
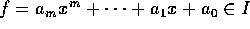とし、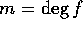
に関する帰納法で示す。
m = 0 ならば、
だから、この場合は良い。
m>0 とする。r<m の時は、e = m-r、
の時は、e = 0 と置くことにすると、
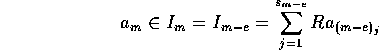
だから、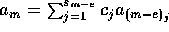
とすると、
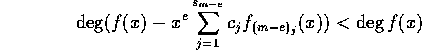
だから、帰納法により、
であることが分かった。
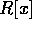の任意のイデアルが、有限生成だから、命題 より、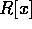
はネーター環である。
ネーター加群の剰余加群はネーター加群であることは簡単に分かるから、ネーター環の剰余環はネーター環である。可換環 S が 可換環 R を部分環として含み、さらに 
に対して、R と、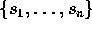
を含む S の部分環は、S であるとする。（このとき、
は、R-上 S を環として生成するという。例えば、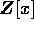
において、x は、
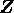-上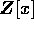 
を環として生成するが、
-加群としては、
すなわち 1次以下の多項式全体が生成されるものである。
R を可換ネーター環とする。R-上有限生成な可換環は、R 上の多項式環の準同型像であるから、R 上の多項式環の剰余環と同型である。従って、ネーター環である。
